Introduction

Dear All,

I would like to share some important updates regarding my blog. We've recently relocated to a new digital home and transitioned to a different web technology. It is with mixed emotions that I make this announcement, but there are compelling reasons behind this move:

• Reduced Maintenance: Over the past 5 years, our old blog had accumulated a significant amount of maintenance work, making it increasingly challenging to manage.

Process Road Map Blog

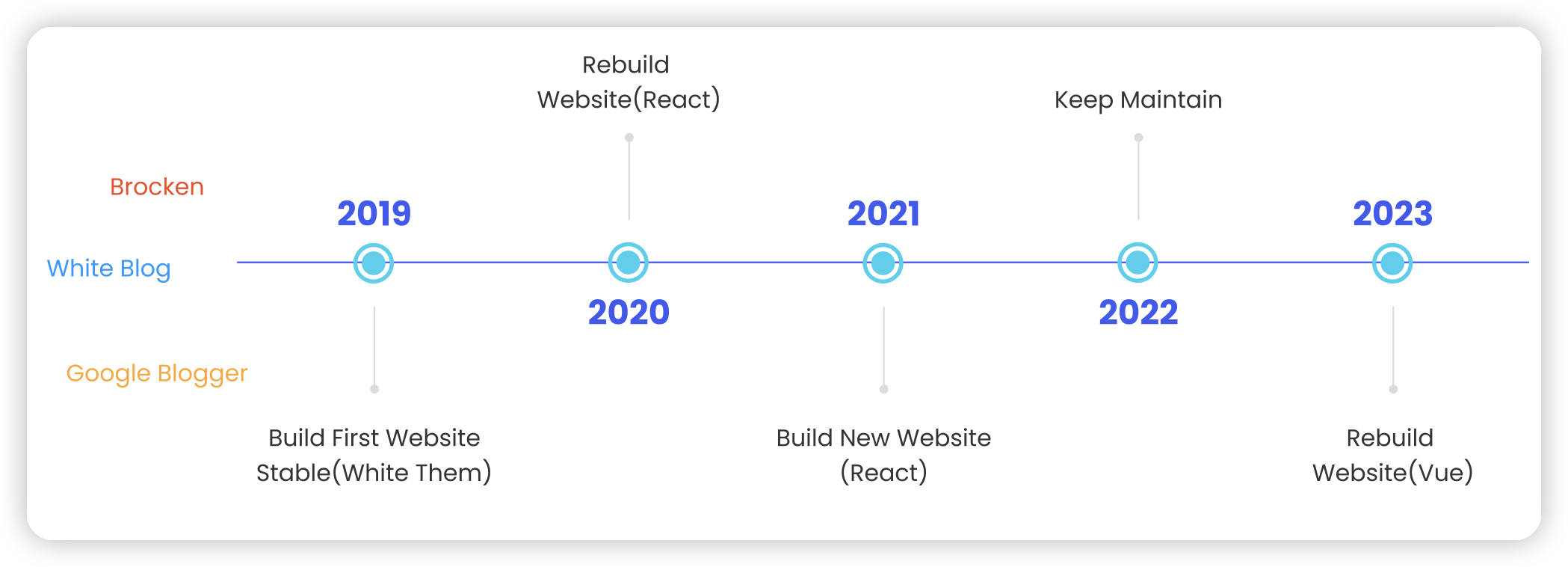
• Slow Loading Times: The packaging process of the old blog was causing slow loading times, affecting the overall user experience.

• Excessive Dependencies: Our previous setup had become heavily dependent on certain elements, making it difficult to implement necessary updates and improvements.

• Persistent Errors: The presence of numerous errors was hindering the blog's functionality, and addressing these issues had become a daunting task.

While we've made this transition, you can still access our old blog at https://chuongmep-beta.vercel.app. In the coming days, we plan to revisit and update some of the older posts, which will also be made available on our new blog.

What Will Remain Unchanged?

Certain core elements of our blog will remain the same:

• Chat Messages
• Comments
• About Me Section
• Hosting Arrangements

What Will Change?

We're excited to introduce several enhancements to our blog:

• Math Formula Support: The new blog will seamlessly incorporate native mathematical formulas for a more interactive experience.

$$\begin{aligned} \text{Mean Squared Error (MSE)} &= \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \\ &= \frac{1}{n} \sum_{i=1}^{n} (y_i - (\beta_0 + \beta_1 x_i))^2 \end{aligned}$$

$$\begin{aligned} \text{Softmax Function for Multi-Class Classification} \\ P(y=i|\mathbf{x}) &= \frac{e^{z_i}}{\sum_{j=1}^{K} e^{z_j}} \end{aligned}$$

Backpropagation in a Neural Network (Partial Derivatives)

$$\begin{aligned} \frac{\partial L}{\partial z^{(L)}} &= \hat{y} - y \\ \frac{\partial L}{\partial W^{(L)}} &= \frac{1}{m} \left(a^{(L-1)}\right)^T \frac{\partial L}{\partial z^{(L)}} \\ \frac{\partial L}{\partial b^{(L)}} &= \frac{1}{m} \sum_{i=1}^{m} \frac{\partial L}{\partial z^{(L)}} \\ \frac{\partial L}{\partial a^{(L-1)}} &= \left(\frac{\partial L}{\partial z^{(L)}}\right) \left(W^{(L)}\right)^T \\ \frac{\partial L}{\partial z^{(L-1)}} &= \frac{\partial L}{\partial a^{(L-1)}} \odot \sigma'(z^{(L-1)}) \end{aligned}$$

• Built with 'bun': We've chosen the 'bun' platform to build our new blog, ensuring a faster and more efficient performance.

bun install
bun run dev
bun run build
...

• Dark Mode Support: Enjoy reading our content in Dark Mode for improved readability.
• Sidebar: The sidebar will now be available on all pages, allowing you to easily navigate through the blog.
• Compare images: it will be useful to wrirte a post compare design.

Before

After

Compare Two Image

• Search: You can now search for specific content on our blog.

• Tags: You can now deep filter posts by tags.

• Zoomable Images: You can now zoom in on images for a more detailed view.

• Code Highlighting: You can now highlight code snippets for improved readability.

• Table of Contents: You can now view a table of contents for each post.

• Can embed component: I can now embed any custome component in post, Example I want add a button:

Conclusion

Finally, my experience is let's make it simple and easy to use, if we go long time, we will have a lot of things to do and it will be difficult to maintain. I hope you will like my new blog and I will try to write more useful articles for you.

Thank you for reading this article.

I recommend you read this book:

Frameworkless Front-End Development: Do You Control Your Dependencies Or Are They Controlling You ?