Introduction
In Dynamo, Vector.AngleAboutAxis is a mathematical function that calculates the angle between two vectors, vector1 and vector2, around a given axis axis.
Getting Started
The axis is defined by a third vector that is perpendicular to both vector1 and vector2. The resulting angle is measured in radians and is positive if the rotation is counterclockwise around the axis and negative if it is clockwise.
The formula for Angle with Axis is:
angle = Math.Atan2(Autodesk.Vector.Dot(Autodesk.Vector.Cross(vector1, vector2), axis), Autodesk.Vector.Dot(vector1, vector2));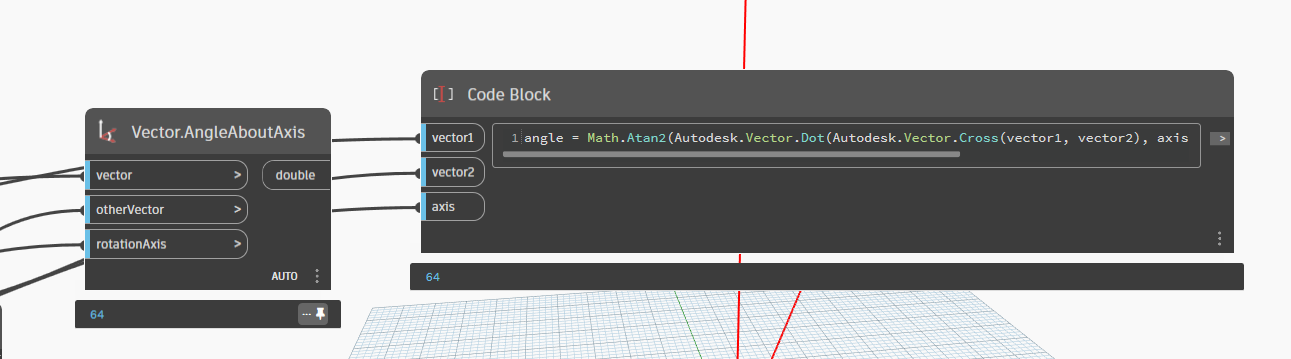
It means that the angle is calculated by the following steps:
Dot() is the dot product of two vectors. The dot product of two vectors is a mathematical operation that produces a scalar value. It is also known as the scalar product or inner product of two vectors.
Cross() is the cross product of two vectors. The cross product of two vectors is a vector that is perpendicular to both of them. The cross product of two vectors is a vector that is perpendicular to both of them.
Atan2() is the four-quadrant inverse tangent function that takes into account the signs of the two input parameters.
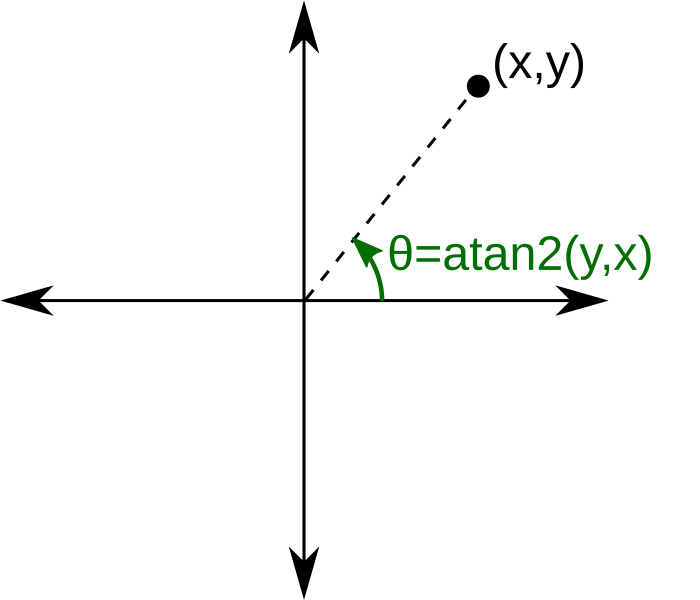
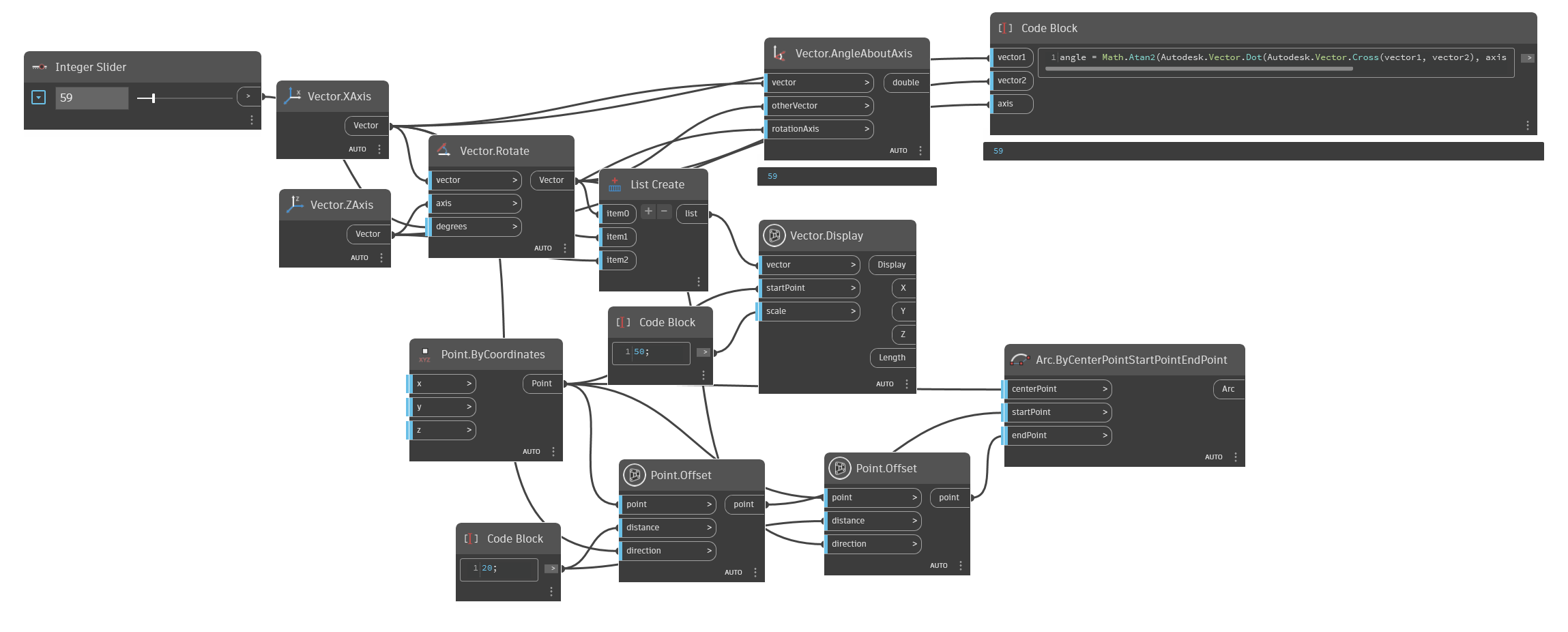
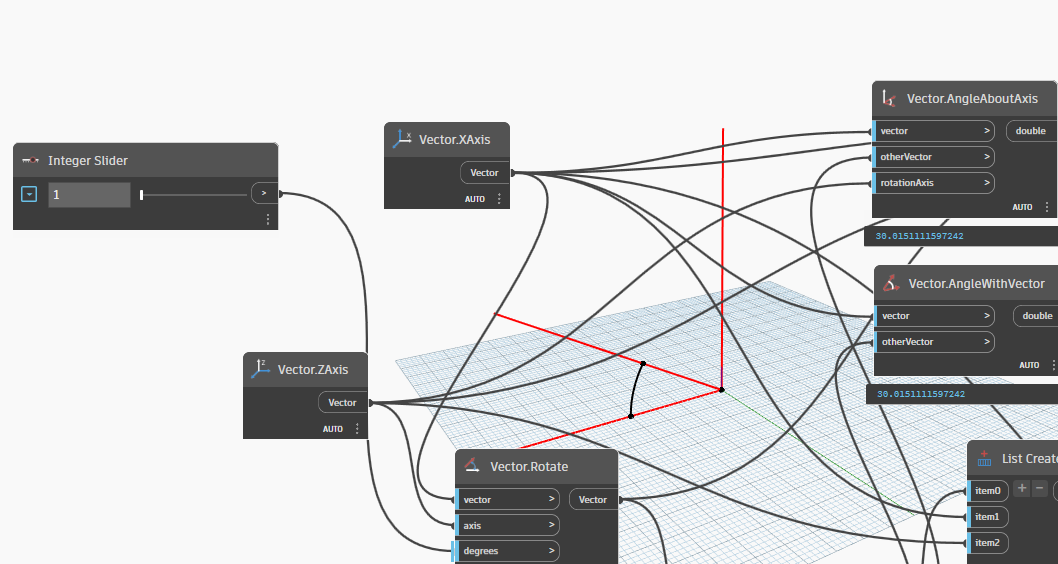
Let's examine the following example, which involves a given vector1, vector2, and axis. In this scenario, Vector1 and Vector2 represent the XAxis, while the Axis represents the ZAxis. Firstly, we rotate Vector1 around the ZAxis to Vector2. Next, we create an Arc.ByCenterPointStartPointEndPoint to quickly determine the angle between Vector1 and Vector2 as we rotate from 0-180 degrees. If the angle is greater than 180 degrees, we can observe that the resulting angle between the two vectors is equal to 360 degrees minus the original angle. This method offers an efficient way to compare the angles between two vectors.
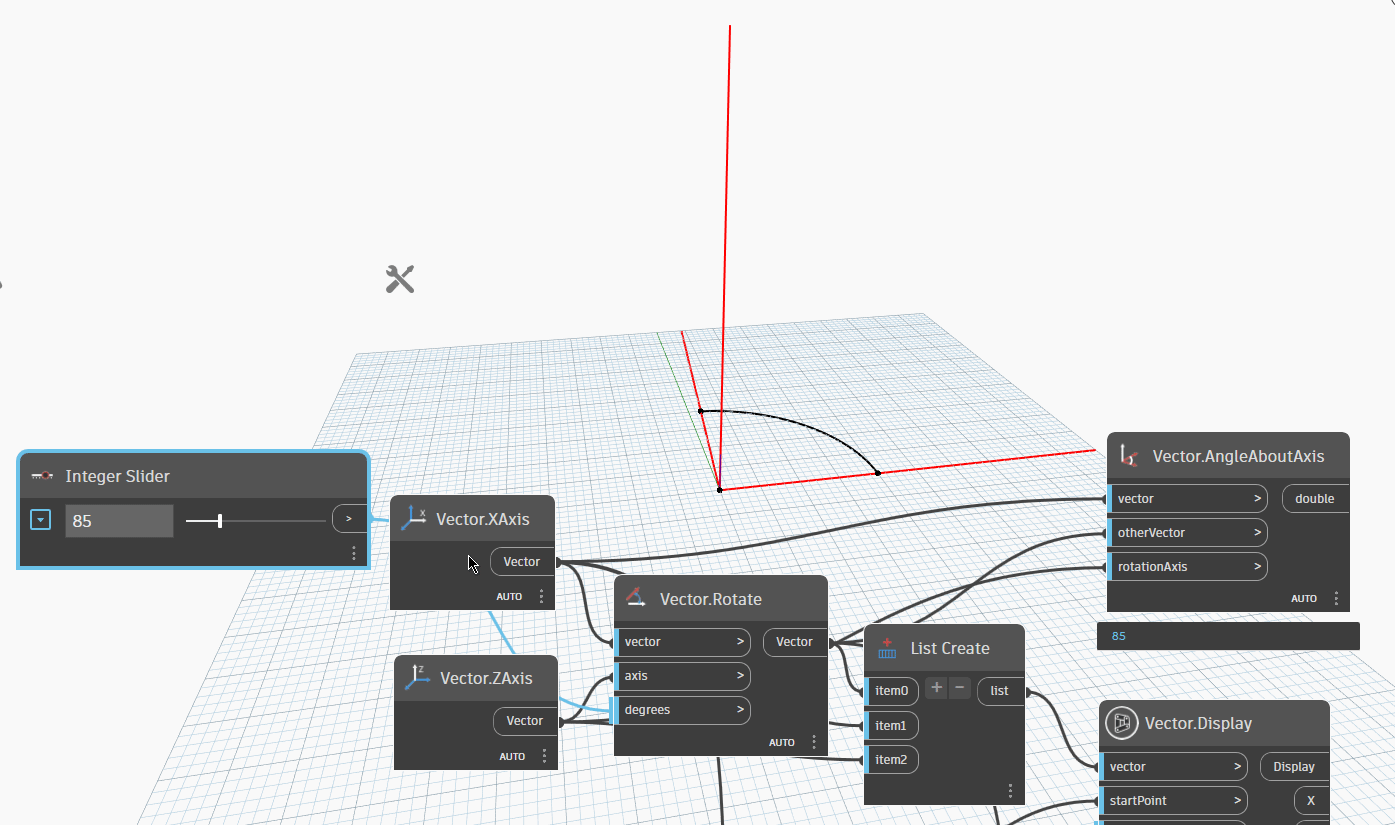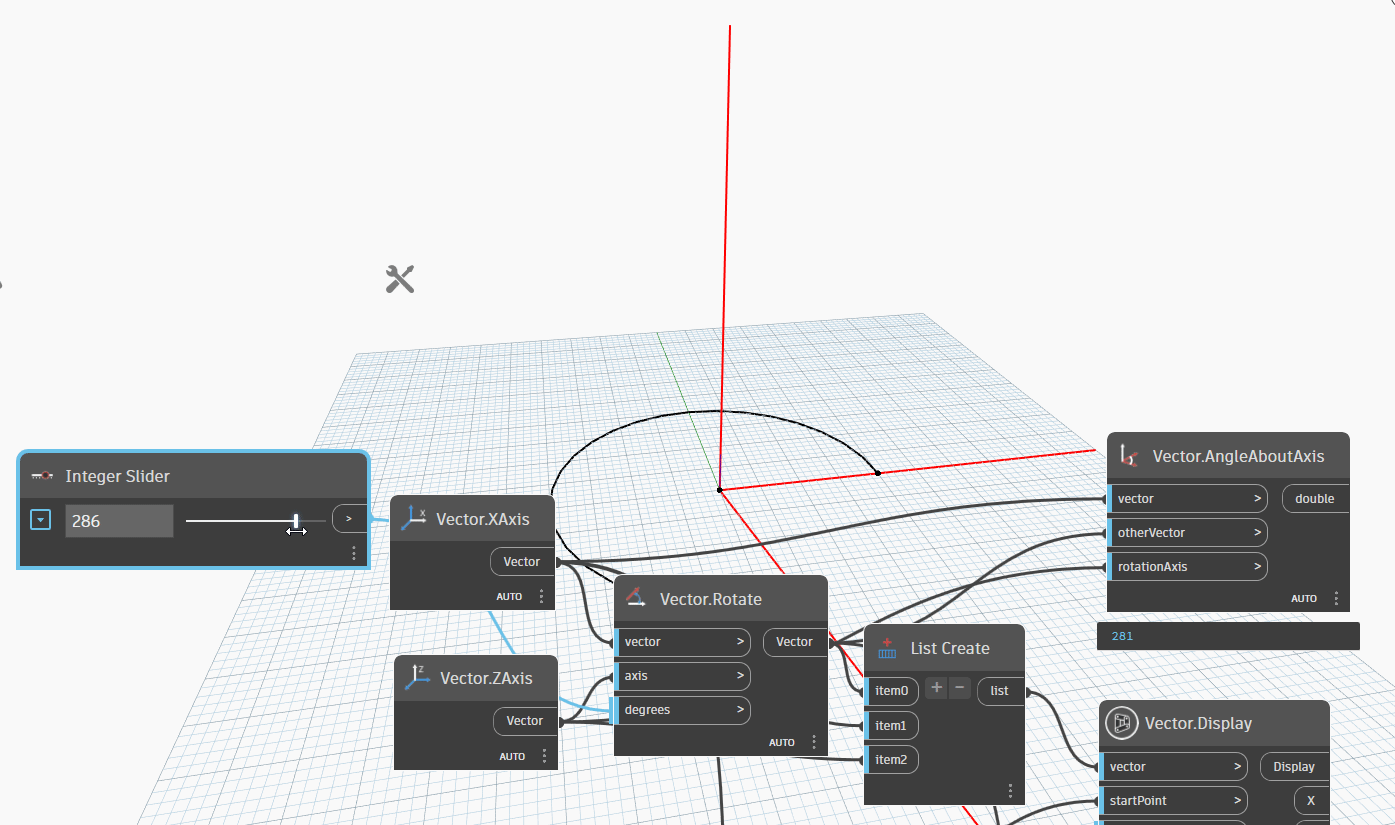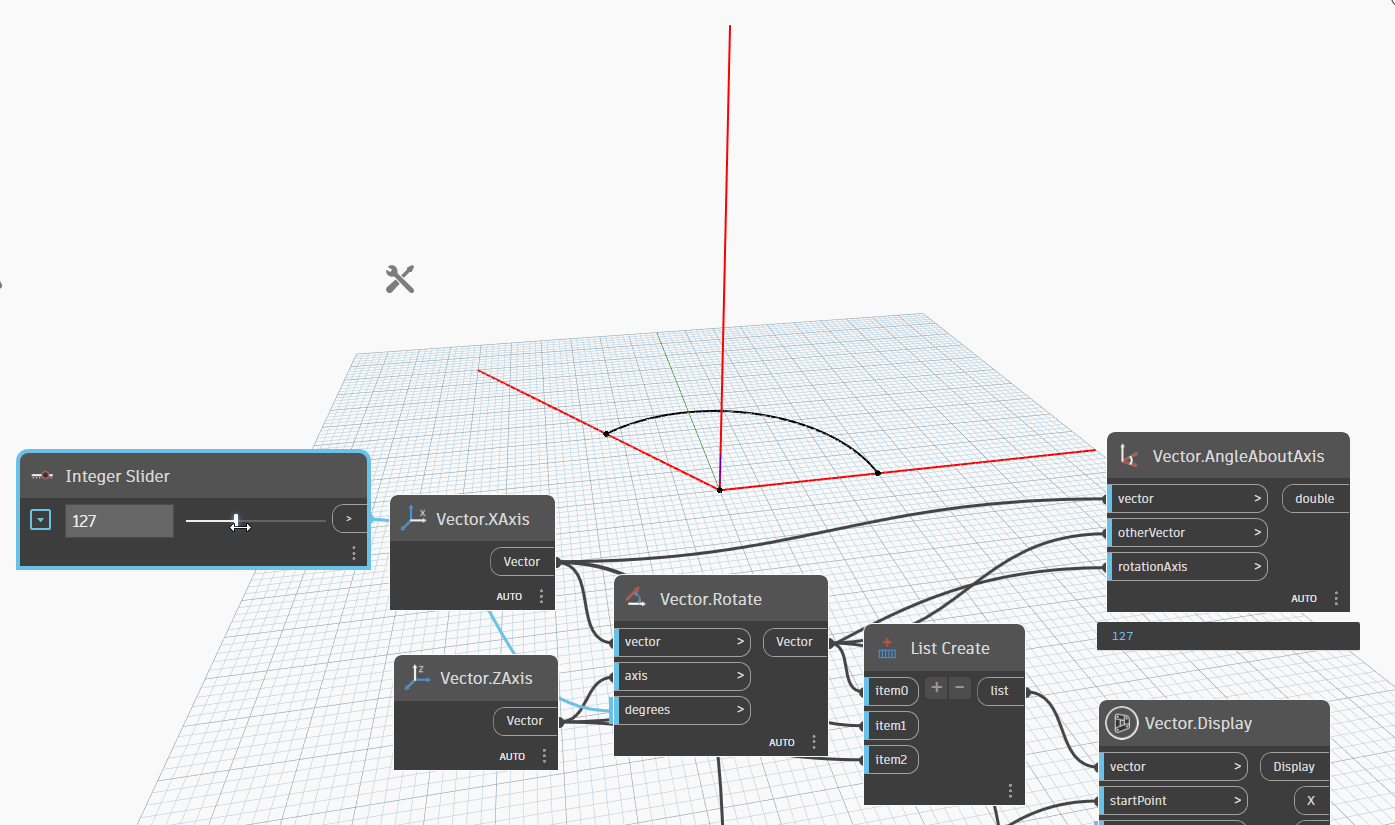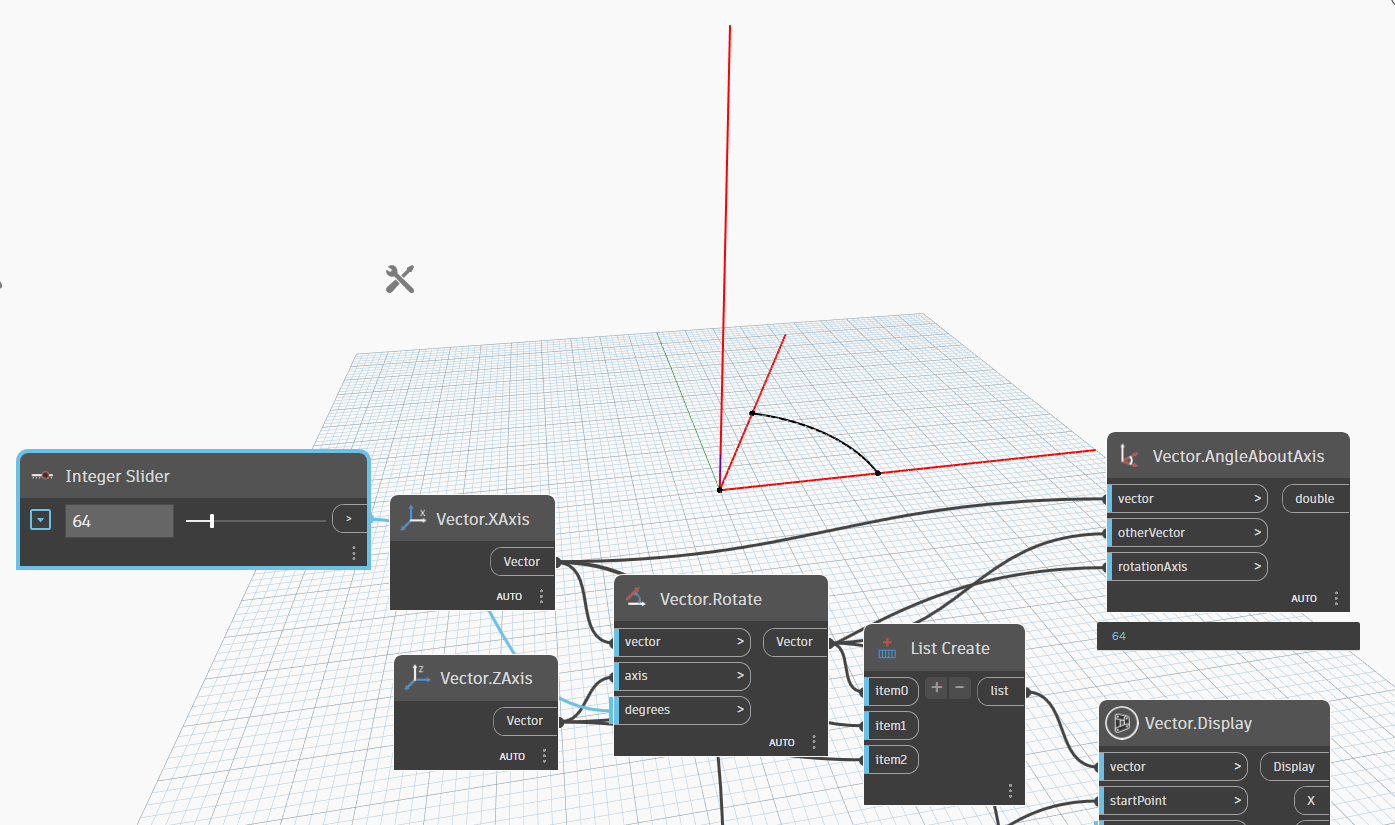
We can see a gif image below to see the rotation of Vector1 around ZAxis to Vector2.
Now, let simple node Vector.AngleAboutAxis by formula:
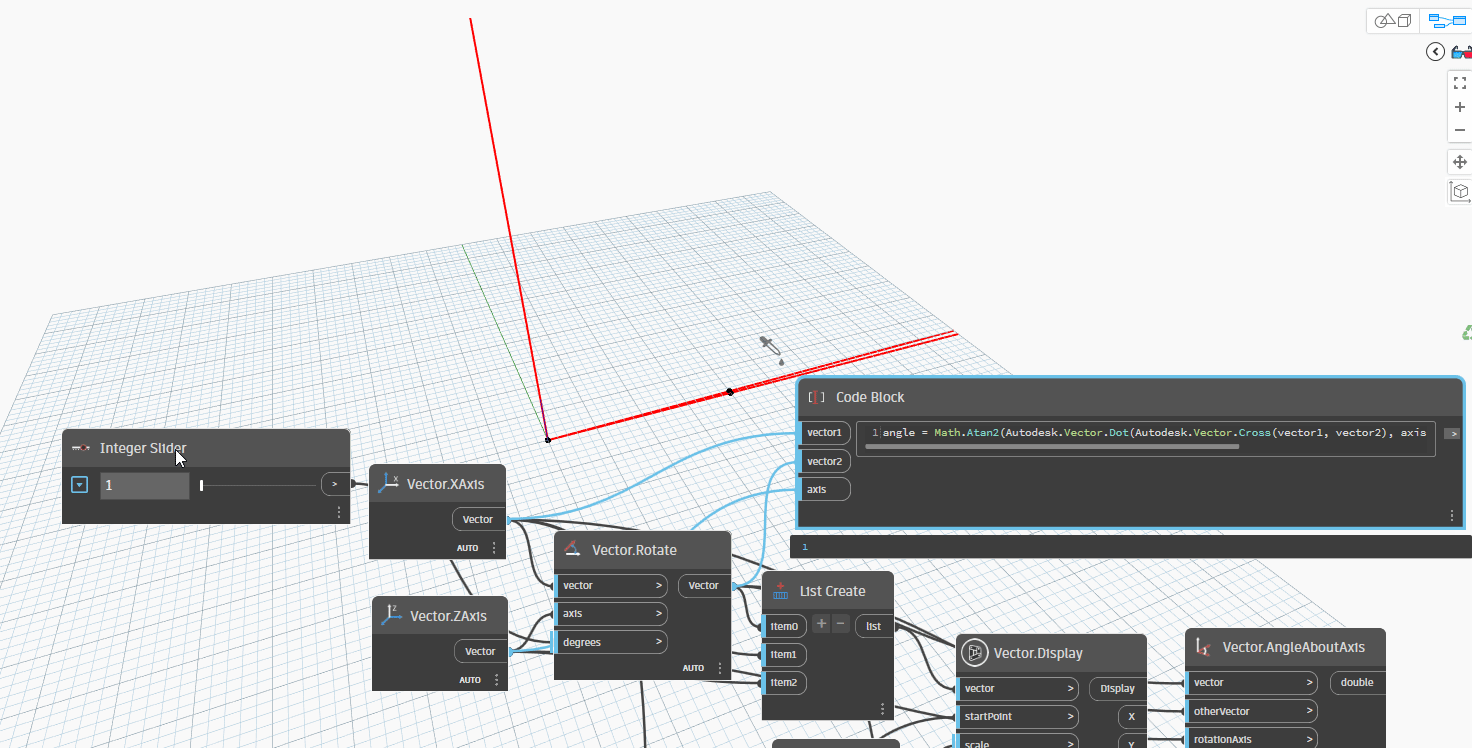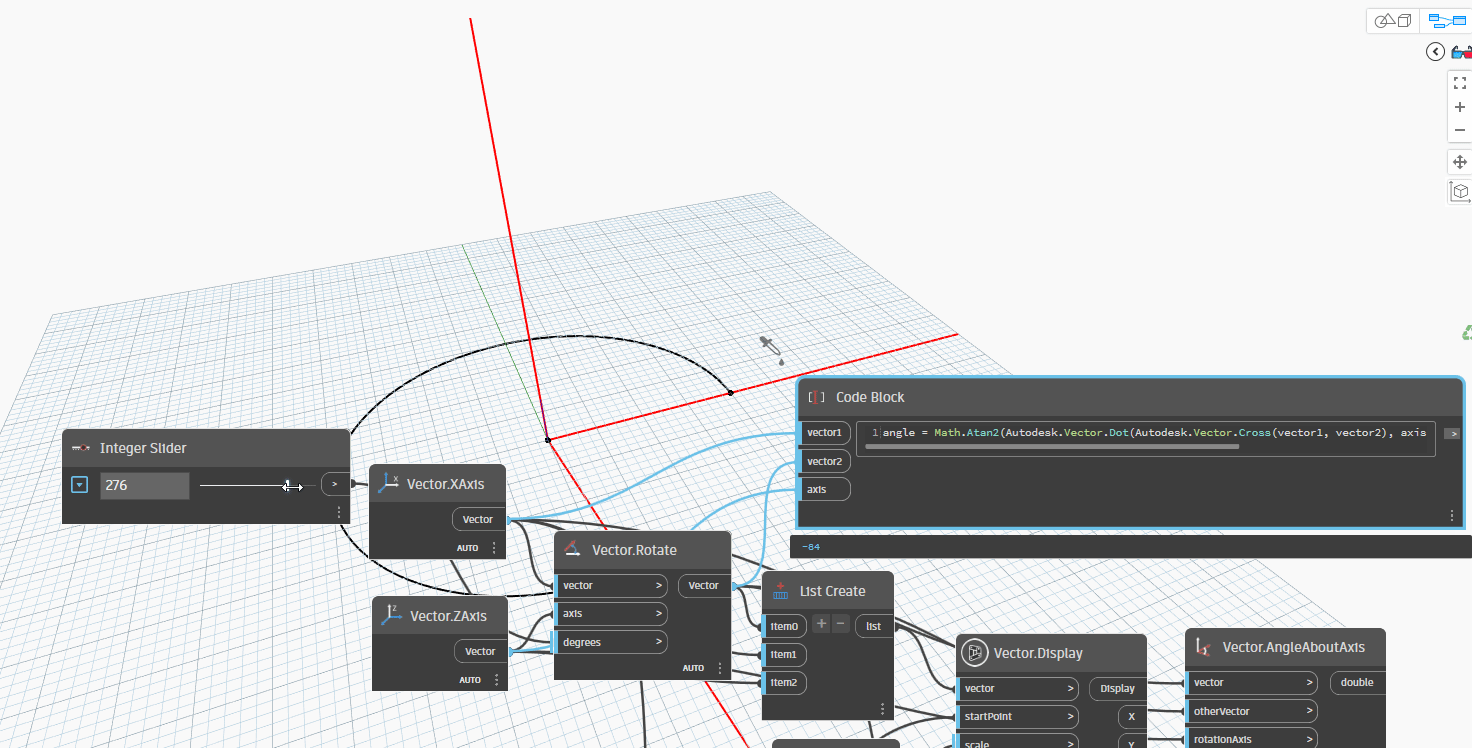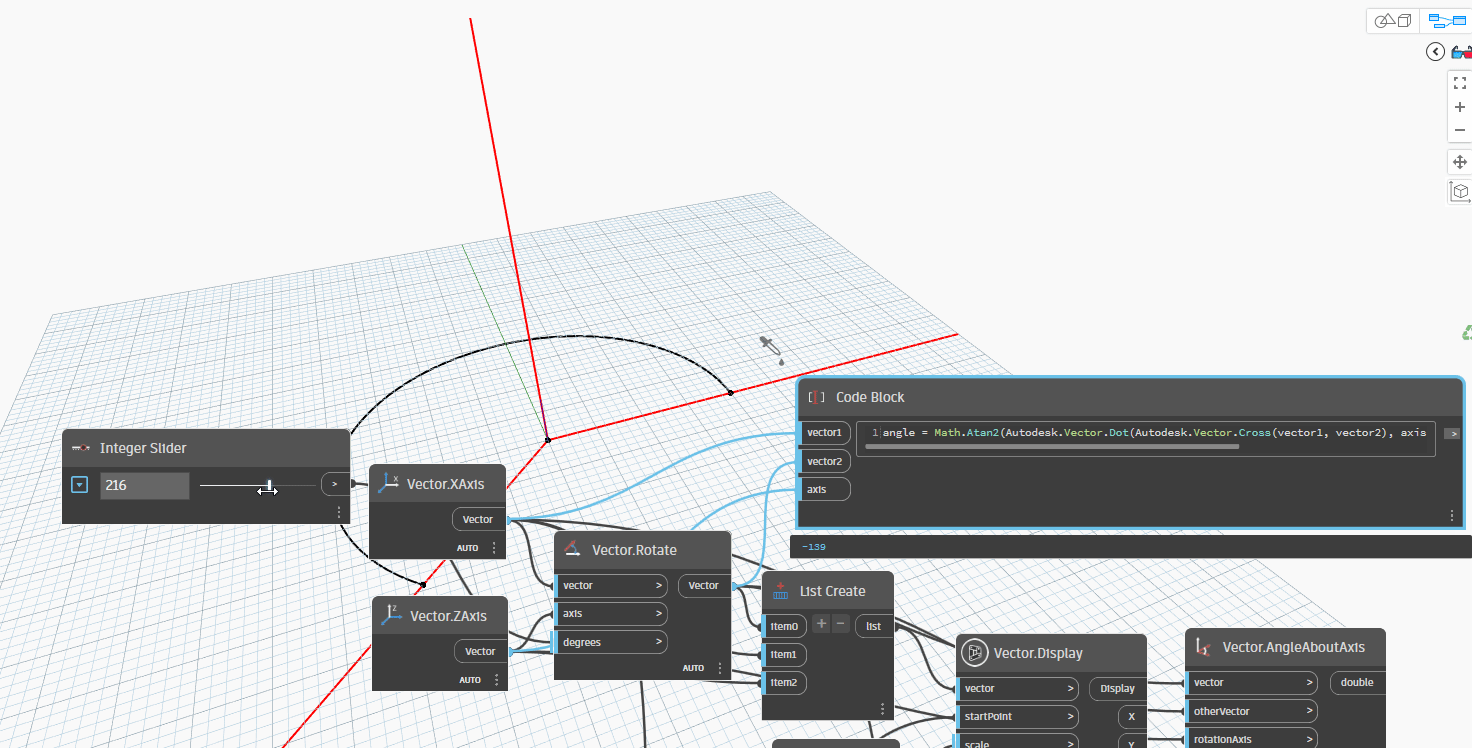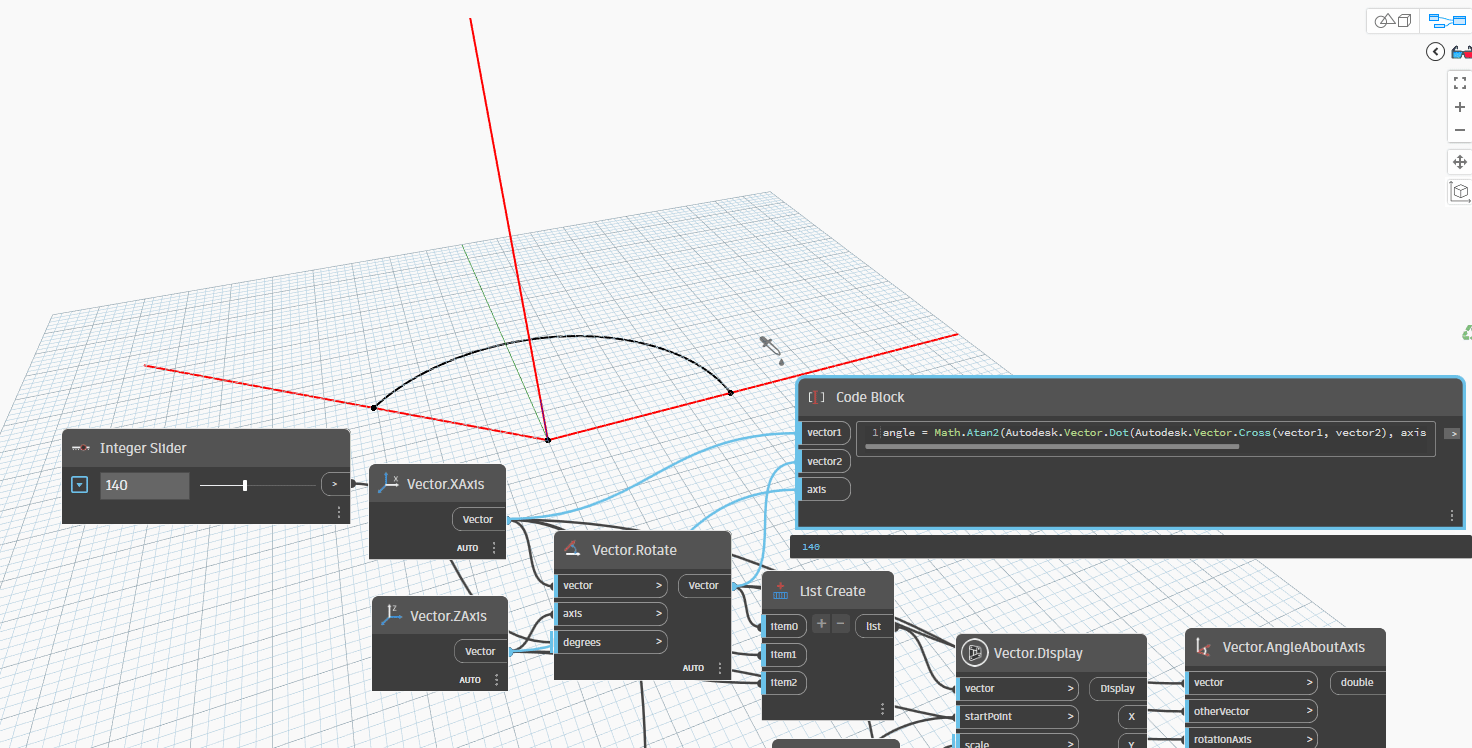
Let's take one more step and attempt to rotate the Axis (ZAxis) by 30 degrees with XAxis around Vector1 to Vector2. This scenario is frequently utilized in 3D modeling for structures such as Pipes, Ducts, and Cable Trays.
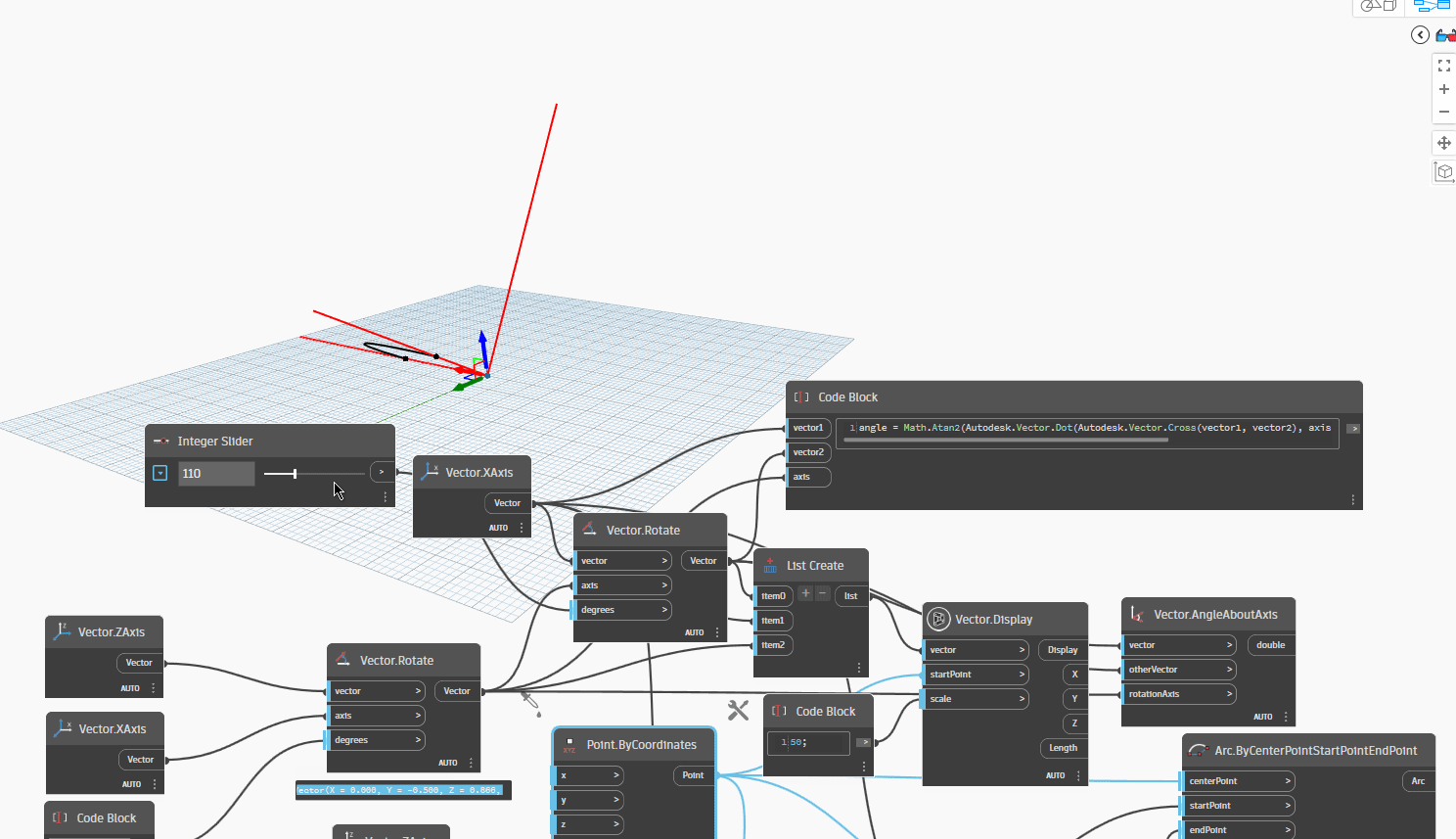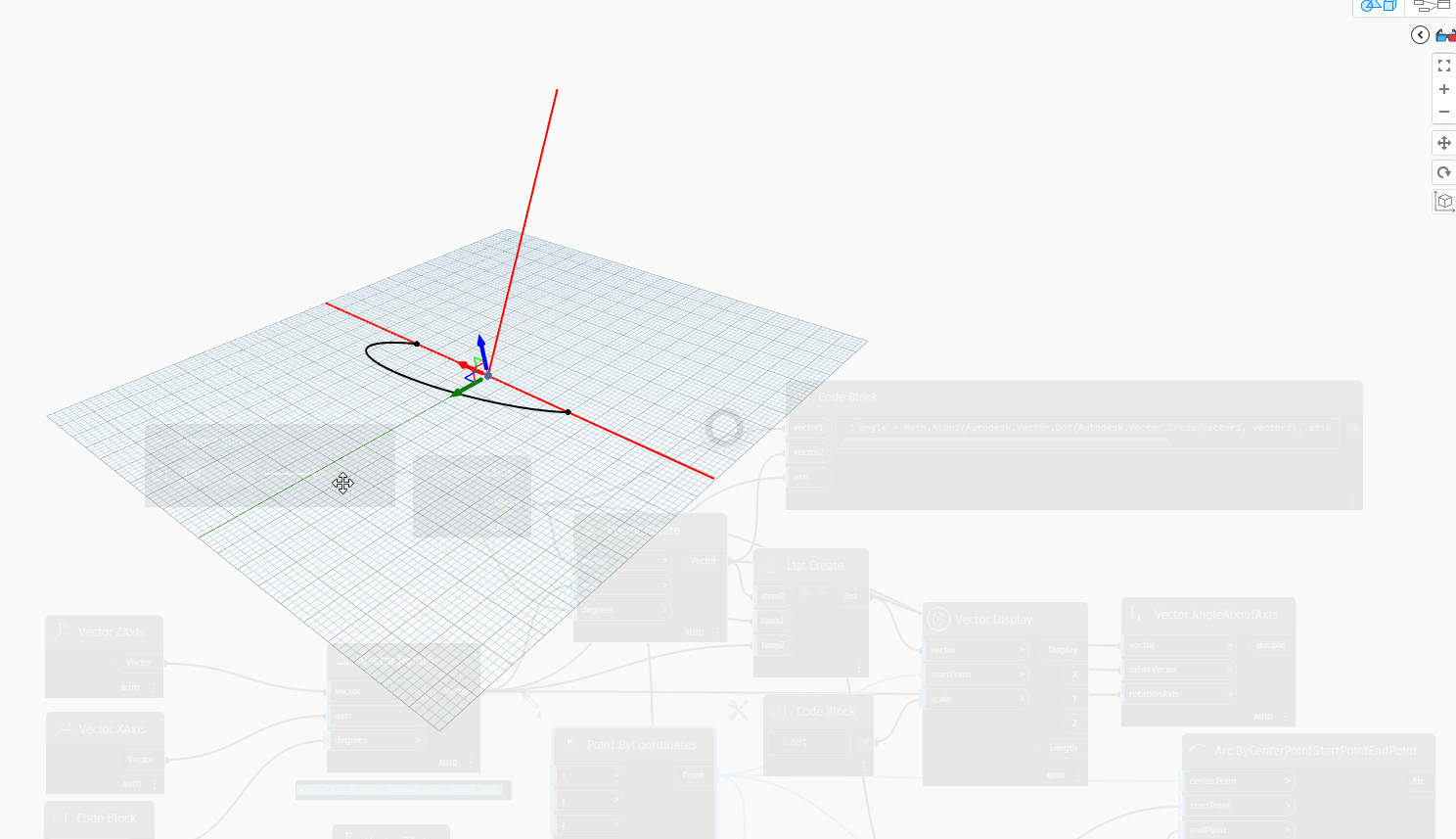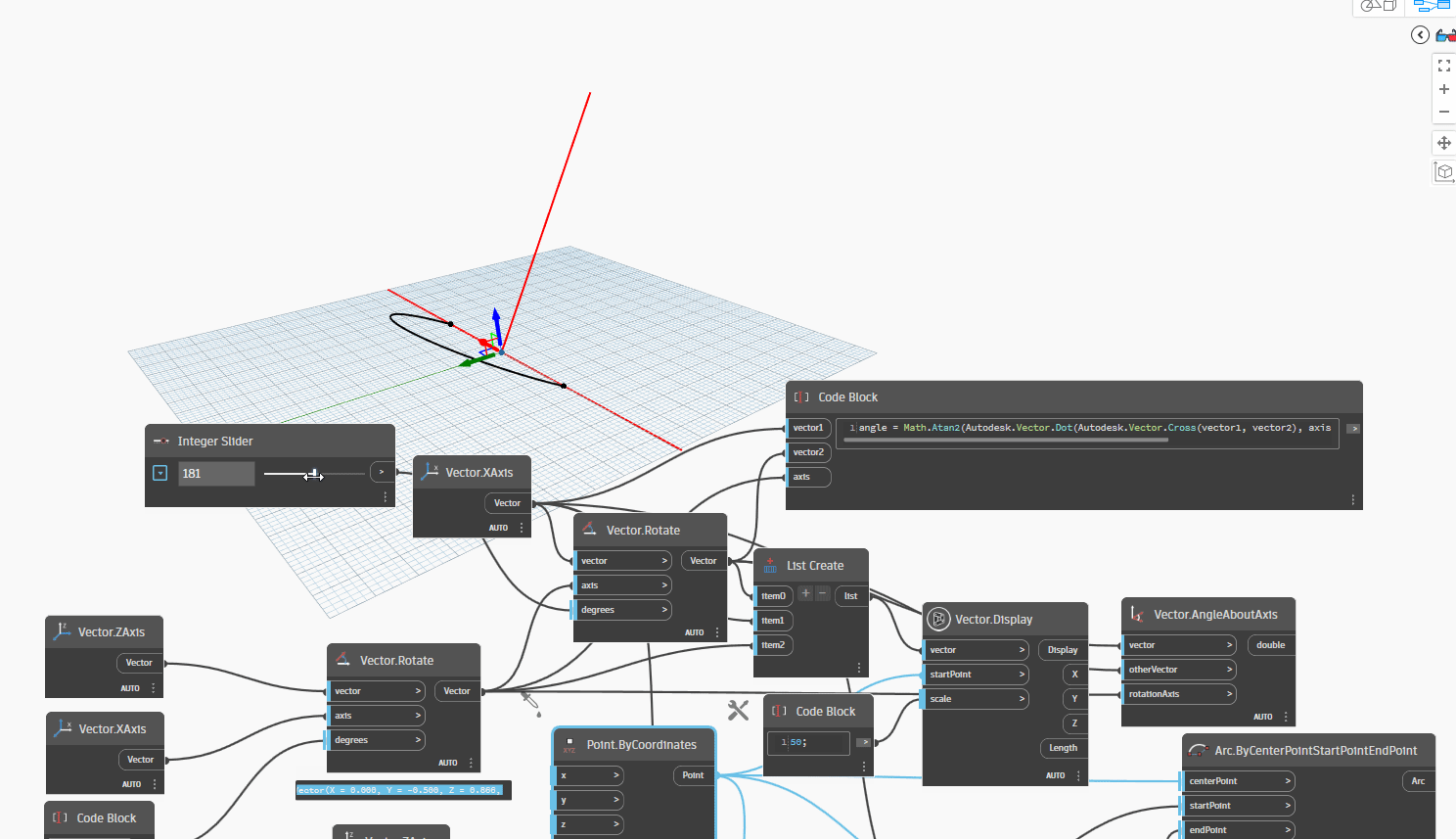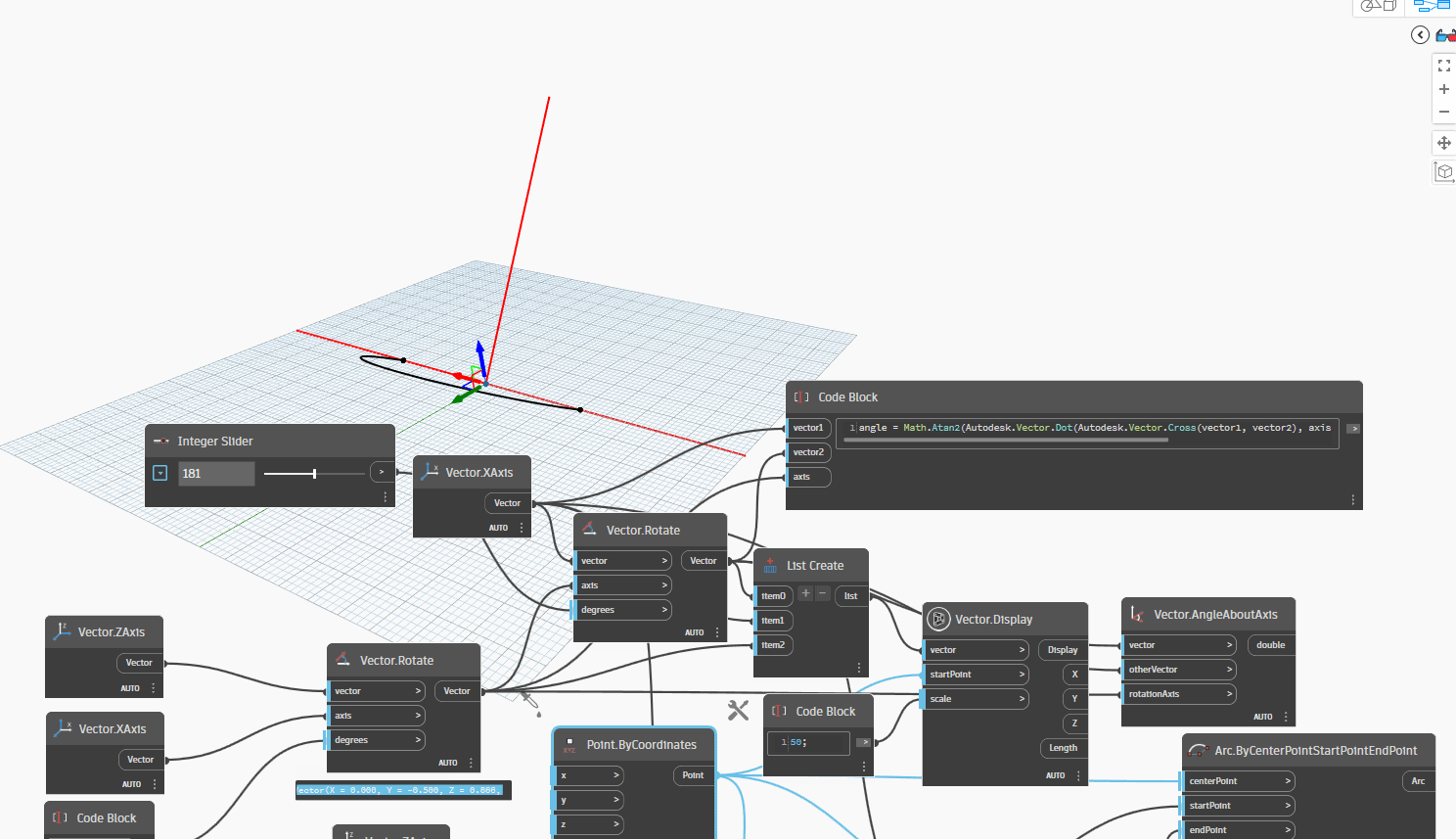
Let's take one more step and try changing the orientation of Vector2(XAxis) by rotating it along the YAxis by -30 degrees, with the rotation axis being the ZAxis. We can achieve this by setting an integer slider to rotate Vector2 by various degrees, ranging from 0 to 360 degrees. The degrees we can try rotating Vector2 by are 45, 90, 135, 180, 225, 270, 315, and 360 degrees.
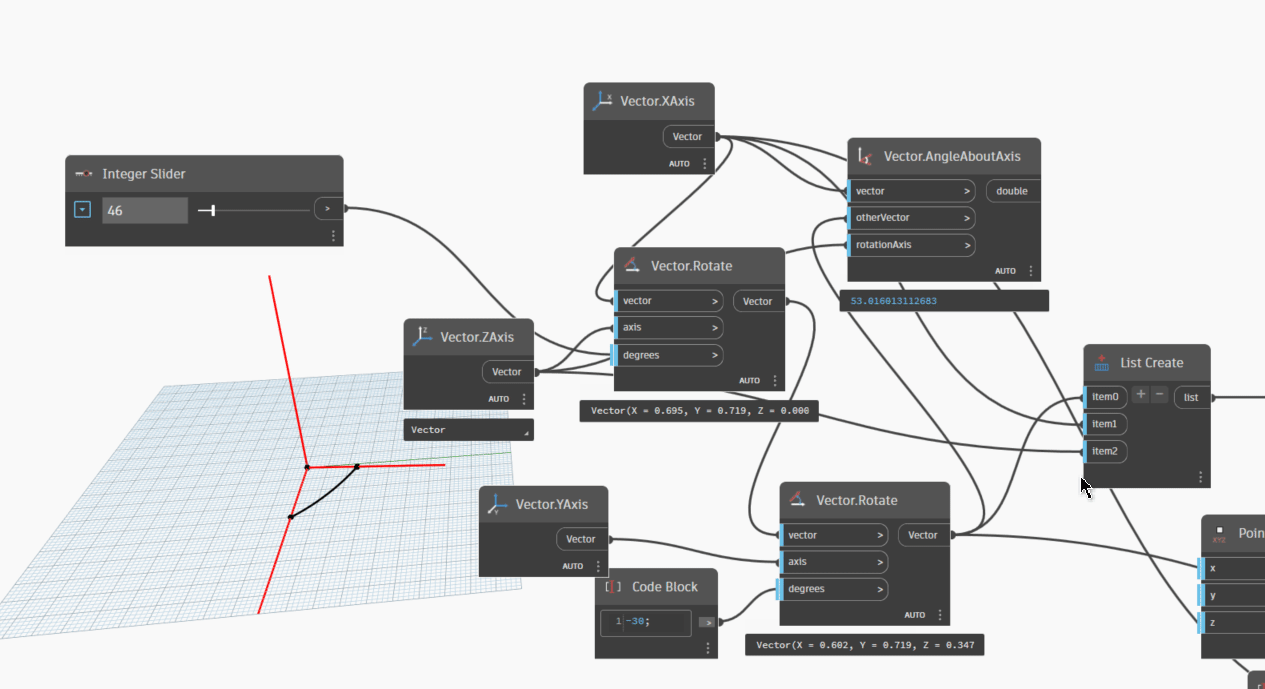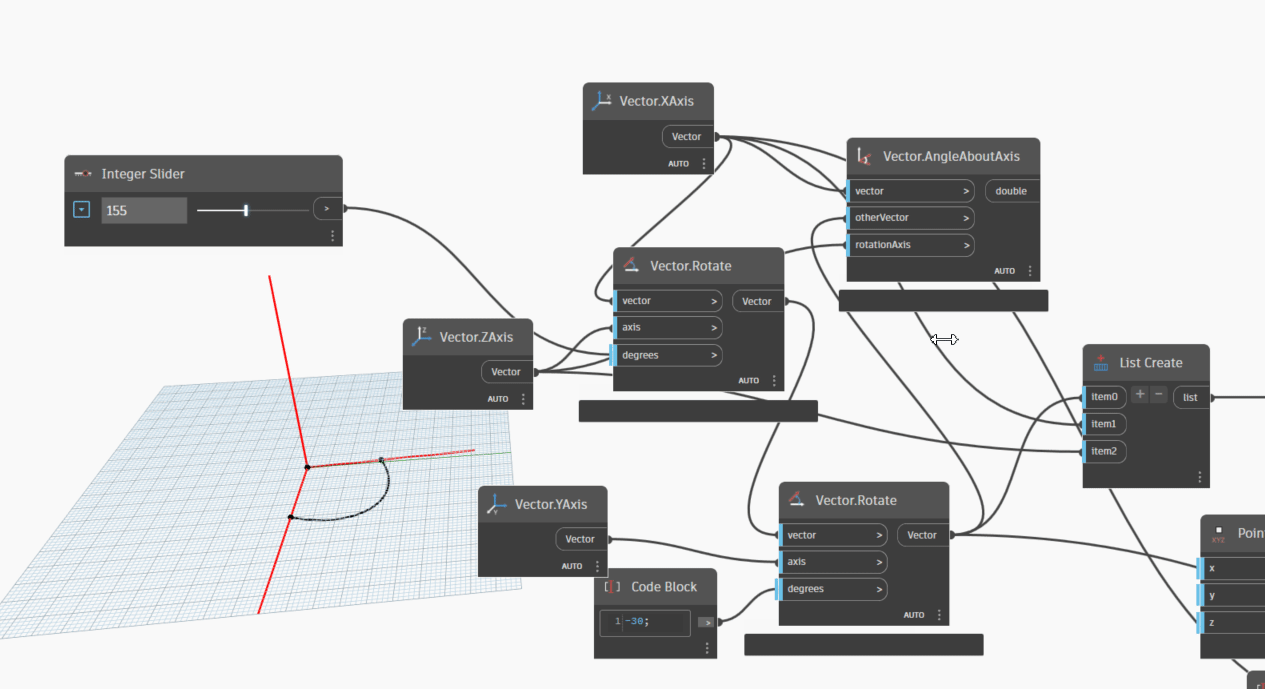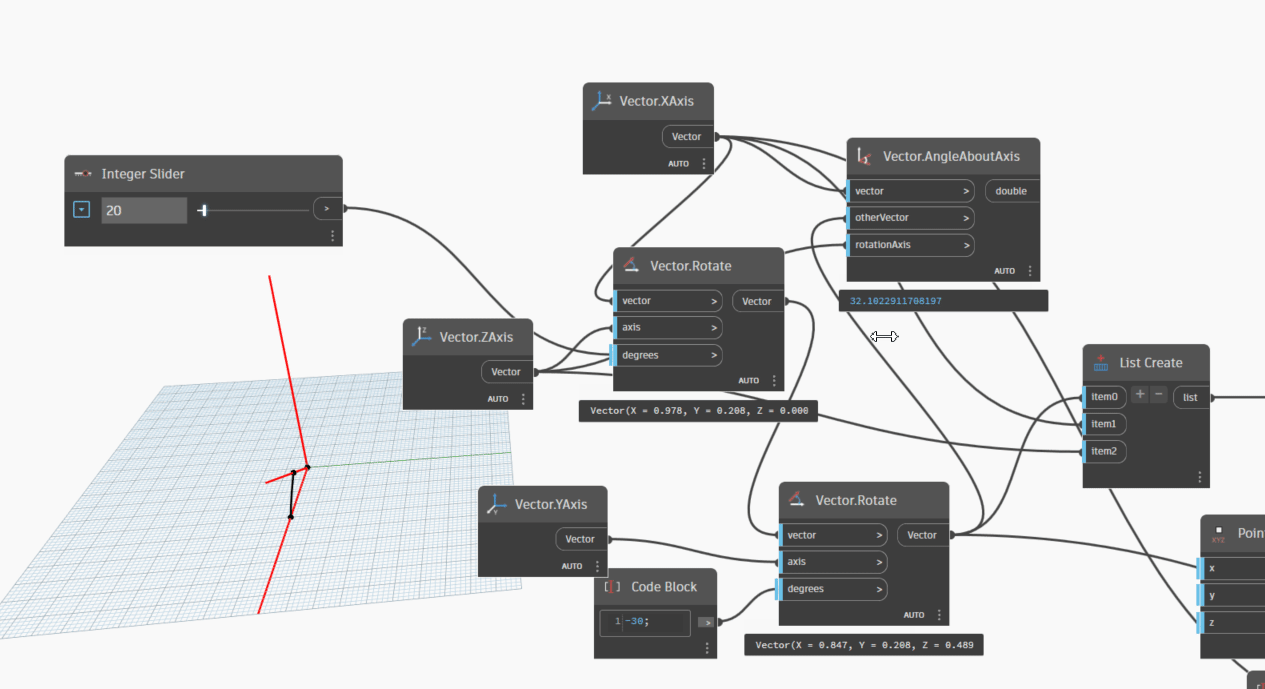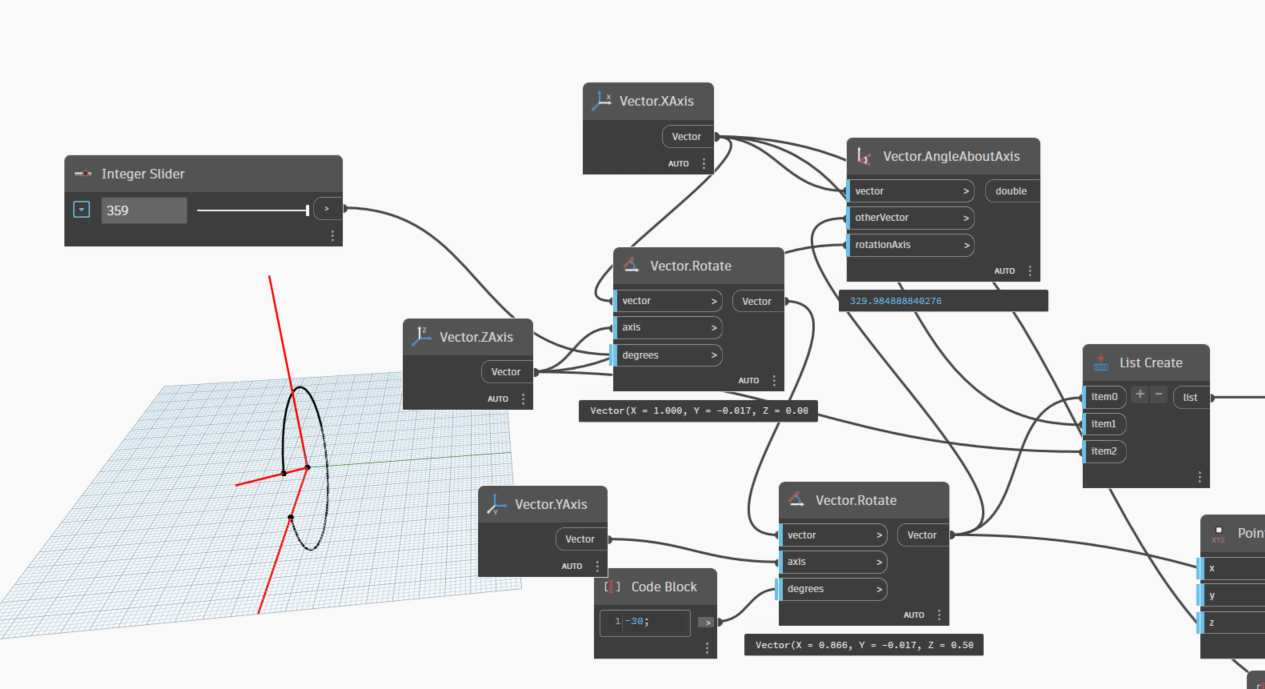
Let's take one more step and incorporate the "Vector.AngleWithVector" node, which provides detailed information about the angle between Vector1 and Vector2. This node will output the angle measurement in two ranges: 0-180 degrees and 180-360 degrees.
- From 0-180 degrees : Vector1 and Vector2 is same degrees with
Vector.AngleAboutAxis. - From Larger than 180-360 degrees : Vector1 and Vector2 is equal value 360 degrees - value of
Vector.AngleAboutAxis.
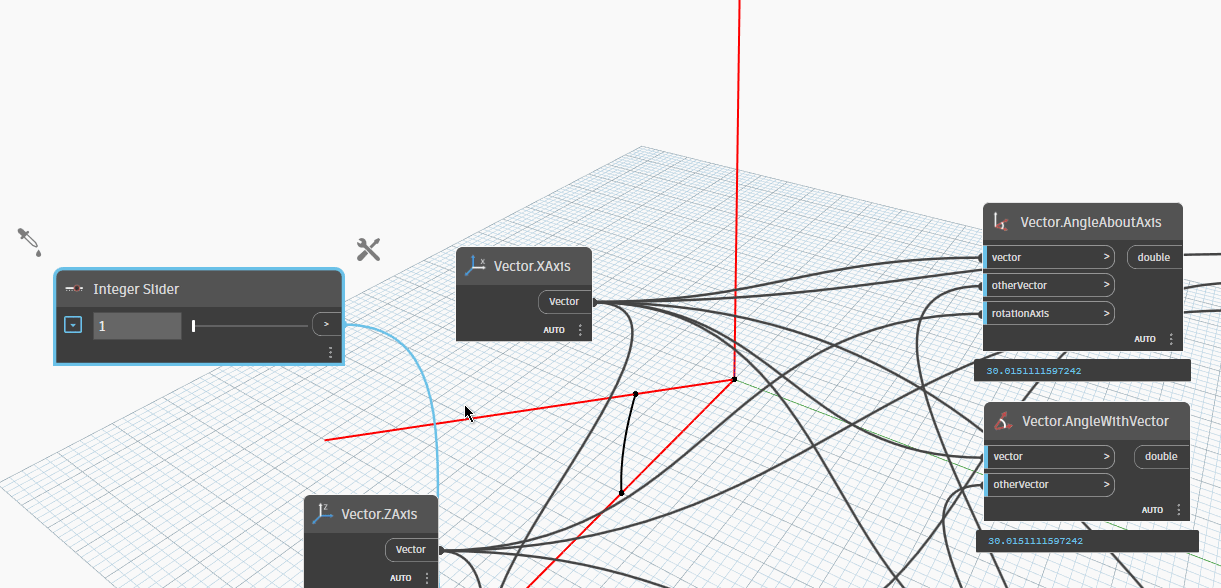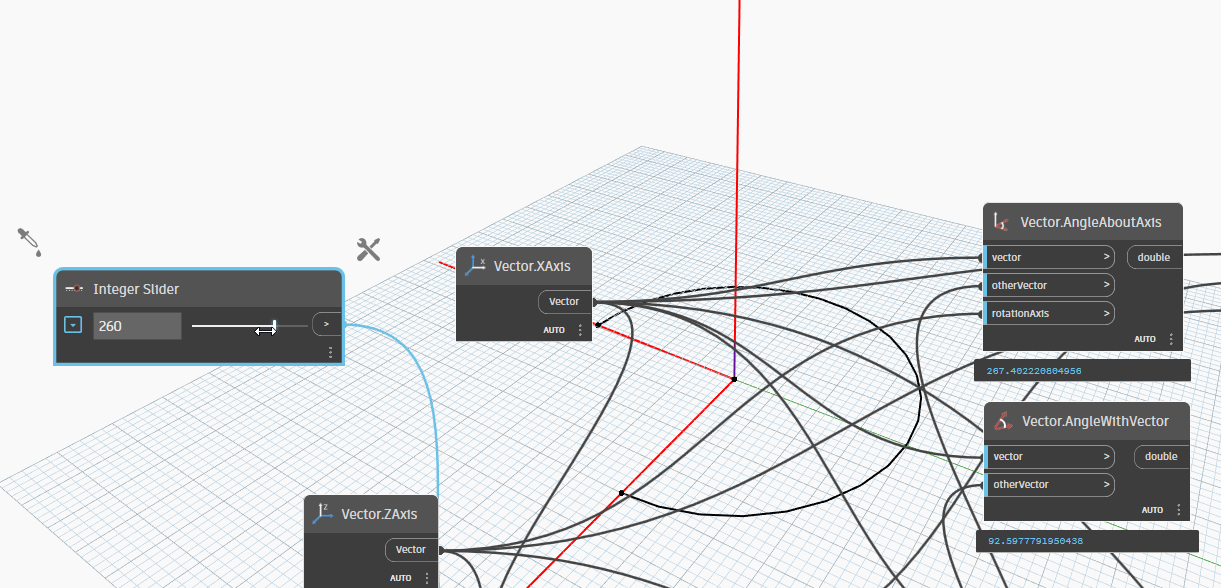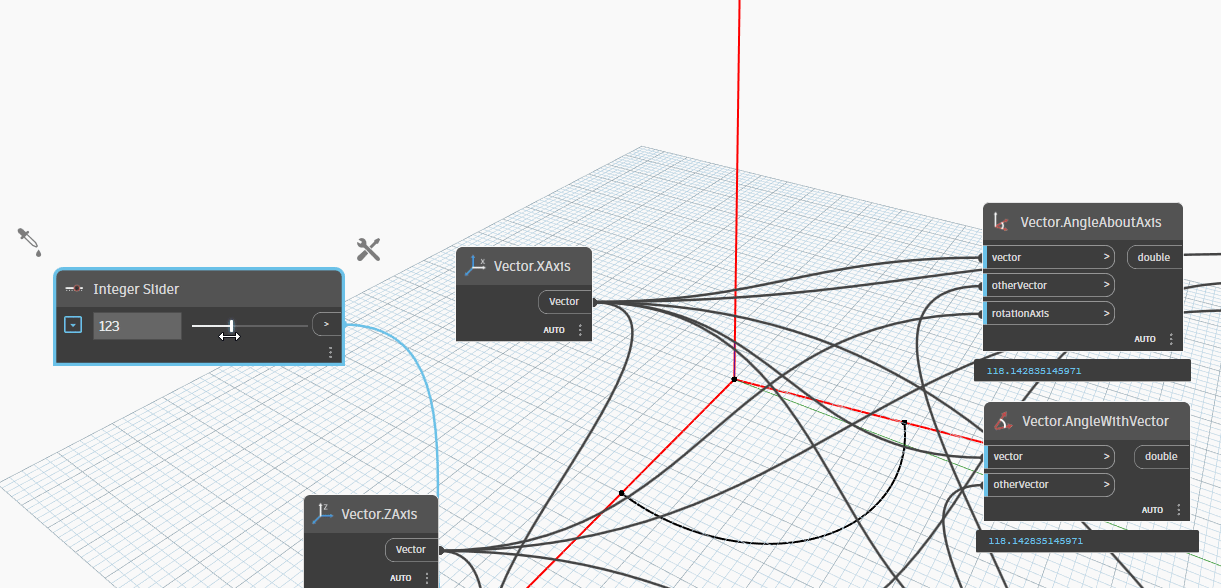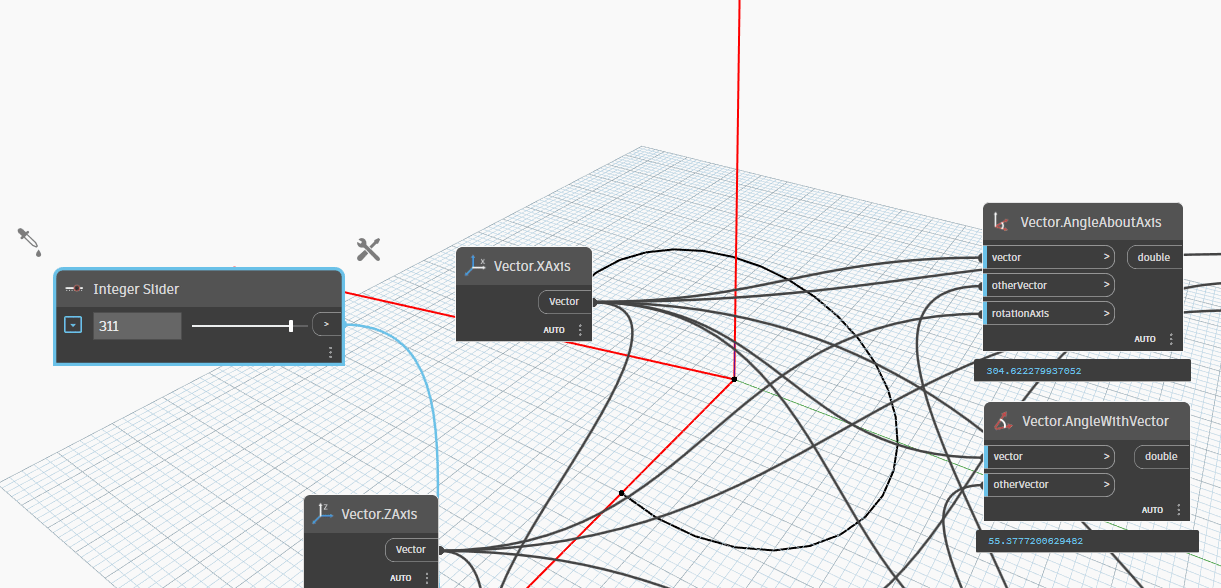
Because we changed Vector2(XAxis) rotate with YAxis is -30 degrees, so result when we change 180 degrees with ZAxis is :
Vector.AngleAboutAxisis 150 degrees.Vector.AngleWithVectoris 150 degrees.
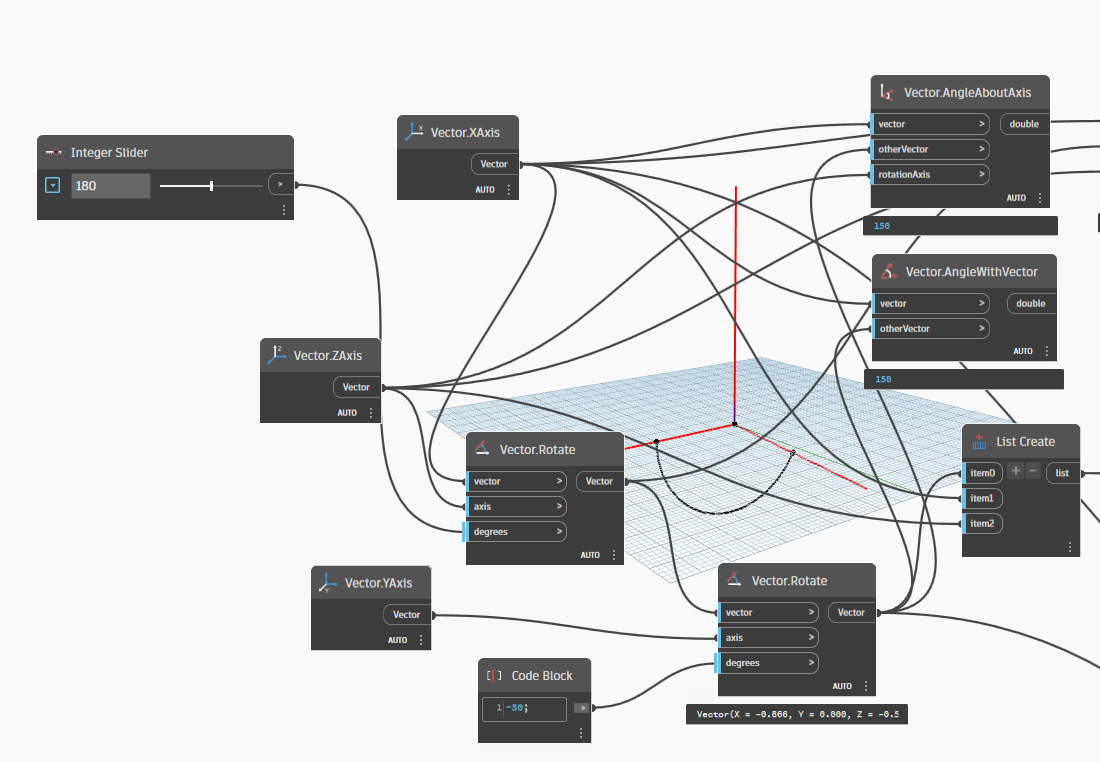
Because we changed Vector2(XAxis) rotate with YAxis is -30 degrees, start at 1 degrees when we change with ZAxis, we can see the result is ~30 degrees.
AngleOnPlaneTo
In Revit API, AngleOnPlaneTo Returns the angle between this vector and the specified vector projected to the specified plane. It also is same with Vector.AngleAboutAxis. but result of AngleOnPlaneTo is in radians, result of Vector.AngleAboutAxis is in degrees.
You can use this method to convert from Rad to Degree by using this formula:
Degree = Radian * 180 / Math.PI
Or you can use this formula to convert from Degree to Rad by using this formula:
Radian = Degree * Math.PI / 180
Pipe Angle About Axis
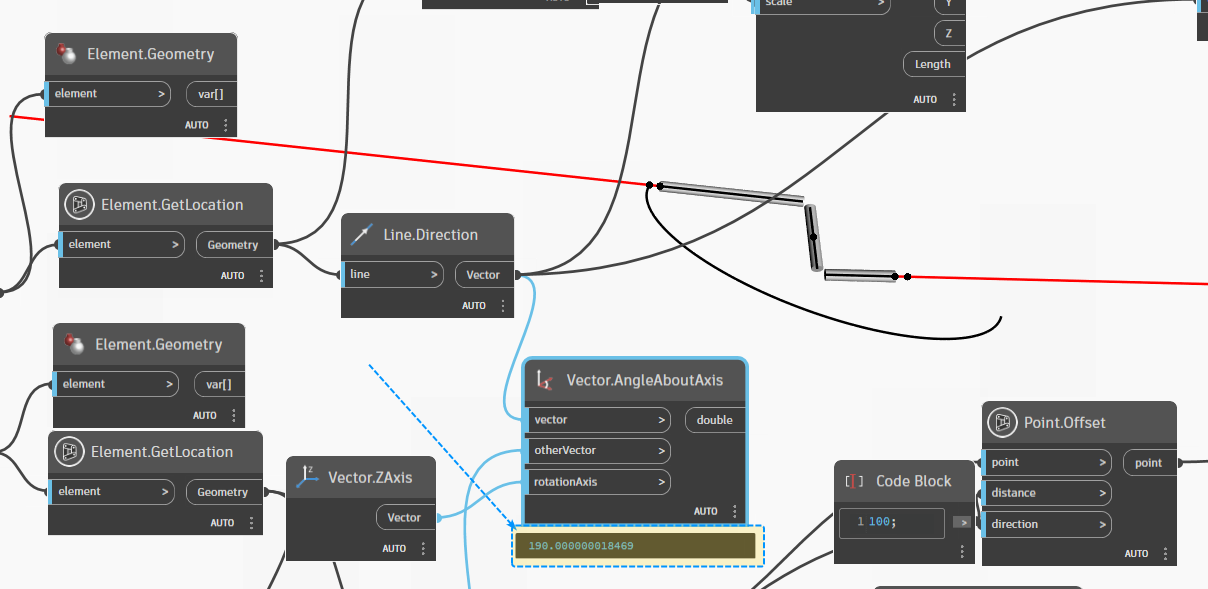
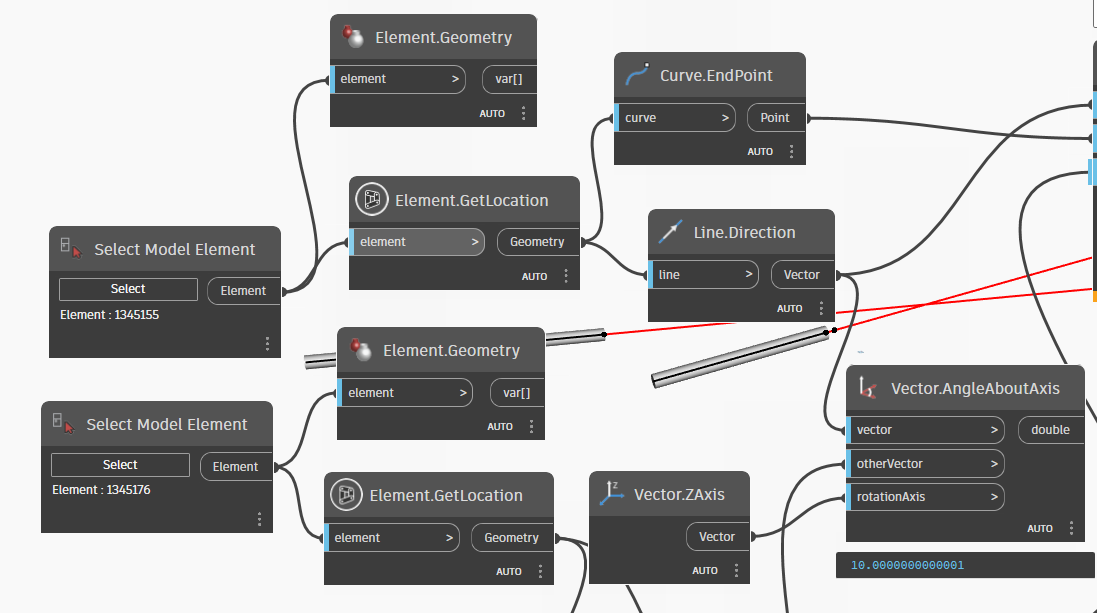
Based on the aforementioned example, we can check the angle between two pipes with the Axis being the ZAxis. If the angle between Pipe 1 and Pipe 3 is exactly 180 degrees, this indicates a favorable scenario for connecting a 90-degree elbow with two pipes that have no slope.
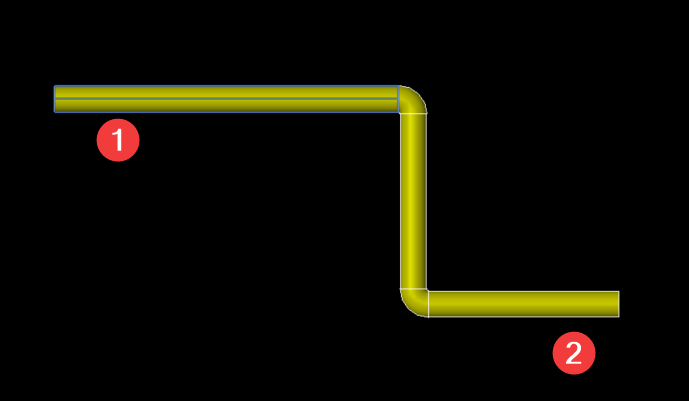
The result is:
Let's consider one more scenario where Pipe 1 has no slope and Pipe 2 has a slope of approximately +/- 10 degrees.
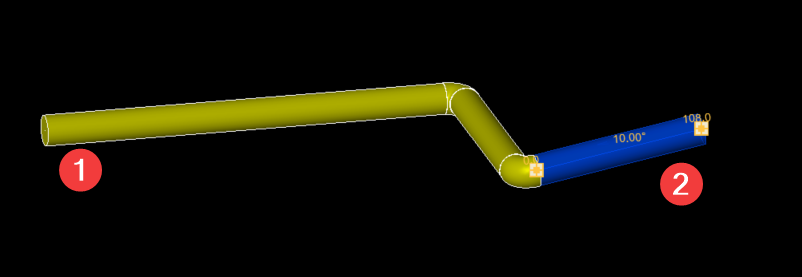
We can now observe that this scenario also presents a favorable outcome for connecting a 90-degree elbow. However, one pipe has no slope while the other pipe has a slope of approximately 10 degrees :
180+10= 190 degree in case two pipe is opposite direction
10= 10 degree in case two pipe is same direction
Conclusion
In summary, Vector.AngleAboutAxis is a useful function in Dynamo for calculating the angle between two vectors around a specific axis, which can be helpful in many applications, including 3D modeling, simulation, and animation.
Download Example File :
Note : Please download package OpenMEP to can run this example file