Giới thiệu
Thuật toán Linear Regression là một thuật toán rất phổ biến và quan trọng trong các mô hình học máy, chúng được ứng dụng rộng rãi trong hầu hết các dự đoán các bài toán có đầu ra là giá trị thực như dự đoán tuổi, dự đoán giá nhà, giá đất, chỉ số lạm phát quốc gia , tốc độ tăng trưởng kinh tế, giá cả ,....
Để dẫn dắt các kỹ sư dễ dàng hơn đến với các mô hình học máy, hôm nay chúng ta sẽ thử cùng tìm ra sự liên hệ giữa độ dốc của đường ống và độ dốc của một đường hồi quy tuyến tính. Trông thì có vẻ không có mối liên hệ nhưng chúng lại có mối quan hệ rất gần gũi với nhau.
Slope Linear Regression
Mô hình Linear Regression có dạng :
Thực chất là một phương pháp học có giám sát trong học máy. Nhưng thay vì dùng ký hiệu là a,b cho phương trình như các bài toán phổ thông, trong học máy chúng ta thường chẩn hóa sang sang w1 cho a và w0 cho b để tiện cho biểu diễn tương tự cho các ma trận biến đổi. Do đó bạn sẽ thường thấy các bài viết về học máy vói phương trình:
Hai trục x,y là hai trục đại diện cho một giá trị của đường thẳng. Thông thường đối với các bài toán học máy, chúng ta sẽ có các điểm rời rạc nhau và rất ít khi tạo ra một đường thẳng lũy tiến.
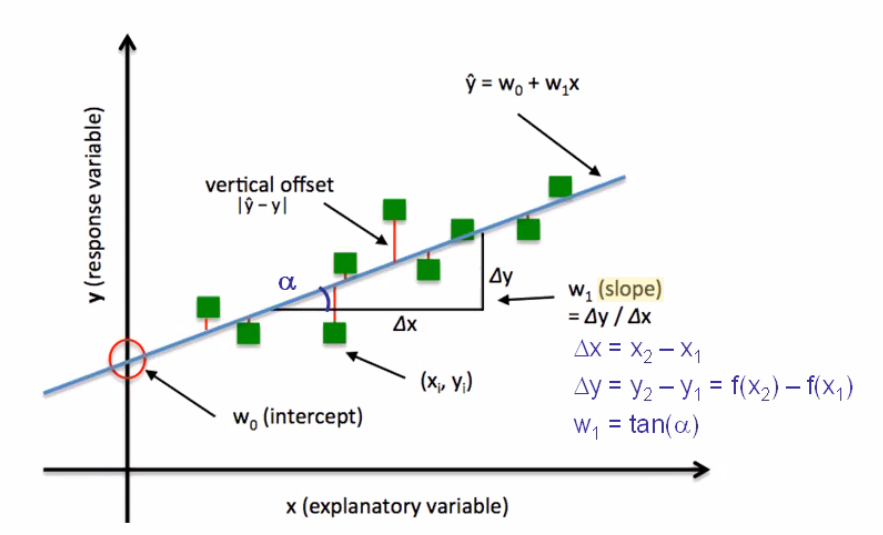
Giá trị độ dốc thường bị thay đổi phụ thuộc vào giá trị mà Y thay đổi khi X tăng thêm 1 đơn vị. Việc nhìn vào độ dốc ta có thể dễ dàng dự đoán nhanh tốc độ lũy tiến và sự phụ thuộc thay đổi của x so với y, xu hướng biến thiên và các mối quan hệ đặc trưng. Ví dụ khi chúng ta làm bài toán điều tra dân số, độ dốc luôn lũy tiến dương, điều đó cho thấy dân số tăng lũy tiến mỗi năm và không có dấu hiệu giảm trừ khi độ dốc âm.
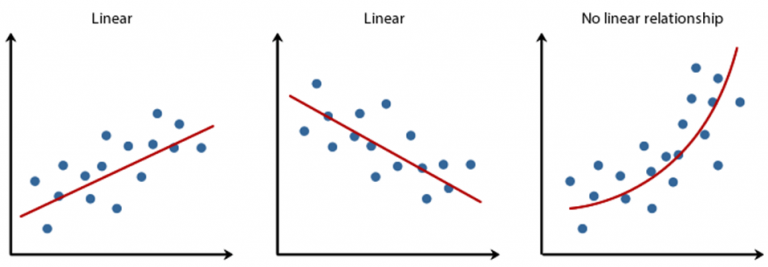
Nếu chúng ta thấy một điểm lạ nằm quá xa so với đường tuyến tính thì chúng ta có thể xem nó là một điểm Outliers. Và đây cũng là một điều khá đau đầu với các kỹ sư học máy để loại bỏ các điểm này nhằm tăng tính chính xác cho mô hình hoặc phát hiện dữ liệu sai sót ngay từ đầu. Có rất nhiều từ ngữ tiếng việt được sử dụng xung quanh như điểm ngoại lai, điểm dị biệt,... Hay thậm chí khi chúng ta khám phá vũ trụ với thuyết vạn vật của Stephen Hawking, chúng ta lại nói về điểm kì dị, liệu chúng có thêm mối liên hệ nào với các lỗ đen ngoài vụ trụ nữa không 😱, có lẽ chúng ta đã đi quá xa so với bài viết này.
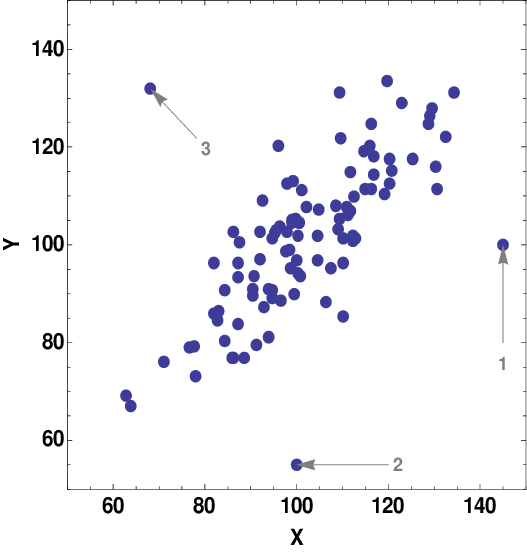
Như vậy qua hình ảnh trực quan bên trên cho ta biết rằng, giá trị độ dốc chính là một hàm tan, vậy thì chúng ta hãy thữ xem mối liên hệ này với ống.
Pipe Slope
Ống trong thiết kế cũng là một đường thẳng lũy tiến. Chúng ta có đủ các thể loại từ ống đứng đến ống nằm la liệt bên trong các bản vẽ, và những ống thoát nước đa phần sẽ đi kèm với độ dốc được thiết kế cụ thể.

Đơn vị thể hiện của ống thường có nhiều dạng khác nhau và việc thay đổi cũng tương đối dễ dàng bên trong Revit, bạn có thể vào Project Unit để thay đổi đơn vị đo lường của ống ứng với độ dốc. Việc thay đổi này trong dự án phụ thuộc rất nhiều vào quy định tiêu chuẩn thể hiện bản vẽ của mỗi công ty.
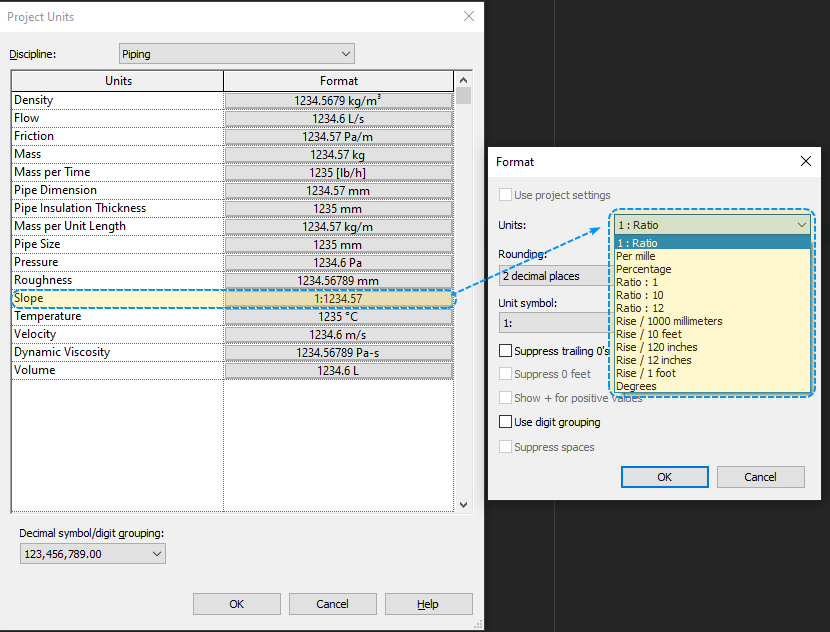
Con số độ dốc 1% chính là tỉ lệ mối quan hệ giữa hai thành phần x và y tương ứng. Do đó nó không được tính bằng bằng radian à kết quả góc là giá trị của một góc tan tương ứng.

Giả sử chúng ta có độ dốc với giá trị là 1 thì góc tương ứng sẽ là 45 độ tương ứng với khoảng Pi/4 và khoảng cách d được tính bằng cân của tổng bình phương hai cạnh góc vuông.

Để kiểm chứng nhanh điều này, bạn có thể sử dụng nhanh vòng tròn lượng giác để xem kết quả hệ số góc theo tan, khoảng 45 độ với kết quả radian là Pi/4.
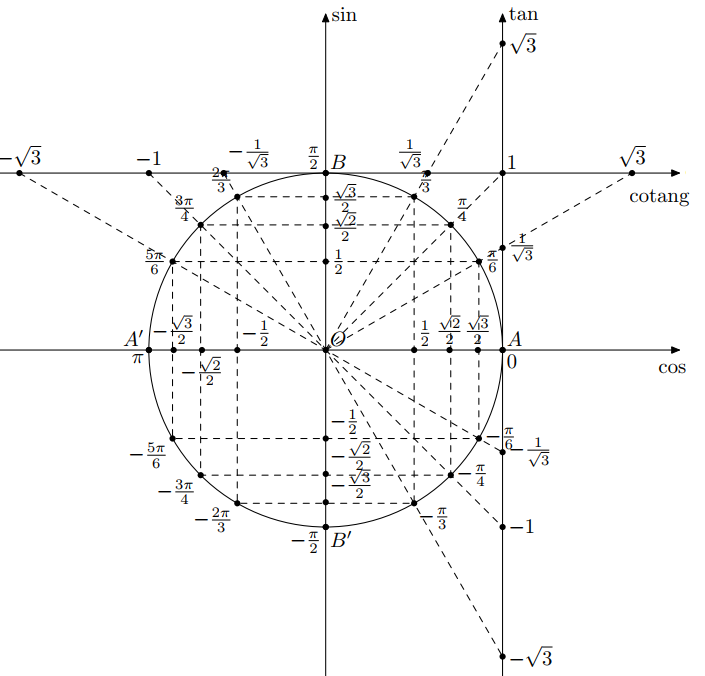
Như vậy việc đã có hai tọa độ điểm đầu và cuối của ống, ta cũng sẽ dễ dàng suy luận lại độ dốc của ống. Và rõ ràng cả bài toán Linear Regression và tìm độ dốc đều có một phương trình đường thẳng, điểm và độ dốc tương ứng.
Tính toán độ dốc
Như vậy việc tìm ra kết quả độ dốc tương đối đơn giản, việc của chúng ta chỉ cần làm là tìm ra các cạnh giữa ống và tính tỉ lệ. Vì là do tính chất tỉ lệ nên việc đơn vị là không quan trọng đối với bài toán này.
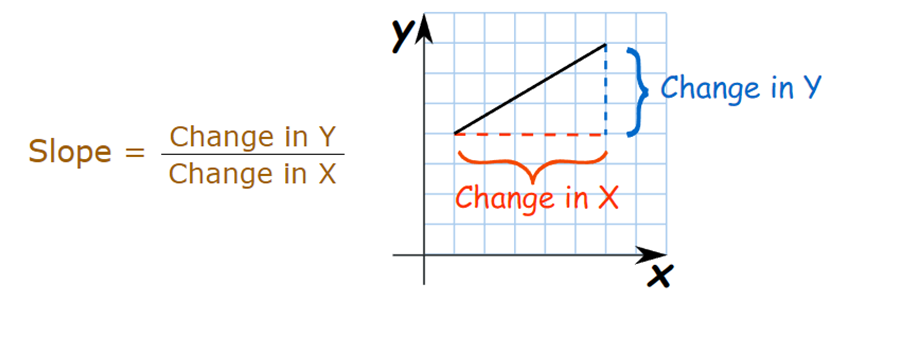
Để rõ ràng hơn, bạn có thể tham khảo qua mô tả toán học chi tiết sau :

Và cuối cùng, việc tính toán độ dốc chỉ đơn giản là cách bạn tìm ra hai điểm trên dưới của ống, chiếu điểm trên của ống vào một mặt phẳng nằm dưới sau đó tính tỉ lệ khoảng cách. Giá trị tỉ lệ khoảng cách chính là giá trị độ dốc cần tìm. Và giá trị góc chính là tan của giá trị đó. Vì trong phần mềm Revit. Thông thường sẽ hiển thị giá trị % nên việc nhân 100 sẽ nhận lại kết quả thực tế.
/// <summary>
/// Return slope of pipe
/// </summary>
/// <param name="pipe">pipe to get slope</param>
/// <param name="digits">The number of fractional digits in the return value.</param>
[MultiReturn("Percent", "Degrees", "Ratio")]
public static Dictionary<string, object?> Slope(Revit.Elements.Element pipe, double digits = 0)
{
Autodesk.Revit.DB.Plumbing.Pipe? internalElement = pipe.InternalElement as Autodesk.Revit.DB.Plumbing.Pipe;
XYZ? bottomPoint;
XYZ? topPoint;
XYZ? startPoint = internalElement.GetCurve().GetEndPoint(0);
XYZ? endPoint = internalElement.GetCurve().GetEndPoint(1);
// if (Math.Abs(endPoint.Z - startPoint.Z) < 0.0001) return 0;
if (startPoint.Z < endPoint.Z)
{
bottomPoint = startPoint;
topPoint = endPoint;
}
else
{
bottomPoint = endPoint;
topPoint = startPoint;
}
Plane plane = Plane.CreateByNormalAndOrigin(XYZ.BasisZ, bottomPoint);
var project = topPoint.ProjectToPlane(plane);
// if (project!.DistanceTo(bottomPoint) < 0.0001) return 0;
double slope = topPoint.DistanceTo(project) / bottomPoint.DistanceTo(project);
double per = Math.Round(slope * 100, (int) digits);
double deg = Math.Round(Math.Atan(slope) * 180 / Math.PI, (int) digits);
return new Dictionary<string, object?>()
{
{"Percent", per},
{"Degrees", deg},
{"Ratio", slope}
};
}
Và điều này không những áp dụng cho ống mà bạn còn có thể mở rộng sang toàn bộ hệ thống các đường khác như Duct, CableTray, Fitting,... Mã bên dưới là mã của một hàm tính toán độ dốc của một đường thẳng thay vì ống, chúng ta chỉ cần sửa đổi một chút :
/// <summary>
/// Return slope of curve
/// </summary>
/// <param name="line">line to get slope</param>
/// <param name="digits">The number of fractional digits in the return value.</param>
/// <returns name="slope">value slope of line</returns>
public static double Slope(Autodesk.DesignScript.Geometry.Line line,double digits=0)
{
Autodesk.DesignScript.Geometry.Point bottomPoint;
Autodesk.DesignScript.Geometry.Point topPoint;
Autodesk.DesignScript.Geometry.Point startPoint = line.StartPoint;
Autodesk.DesignScript.Geometry.Point endPoint = line.EndPoint;
if (Math.Abs(endPoint.Z - startPoint.Z) < 0.0001) return 0;
if(startPoint.Z<endPoint.Z)
{
bottomPoint = startPoint;
topPoint = endPoint;
}
else
{
bottomPoint = endPoint;
topPoint = startPoint;
}
Autodesk.Revit.DB.Plane plane = Autodesk.Revit.DB.Plane.CreateByNormalAndOrigin(XYZ.BasisZ,bottomPoint.ToXyz());
XYZ? project = topPoint.ToXyz().ProjectToPlane(plane);
if(project!.DistanceTo(bottomPoint.ToXyz())<0.0001) return 0;
double slope = topPoint.ToXyz().DistanceTo(project) / bottomPoint.ToXyz().DistanceTo(project);
return Math.Round(slope * 100,(int)digits);
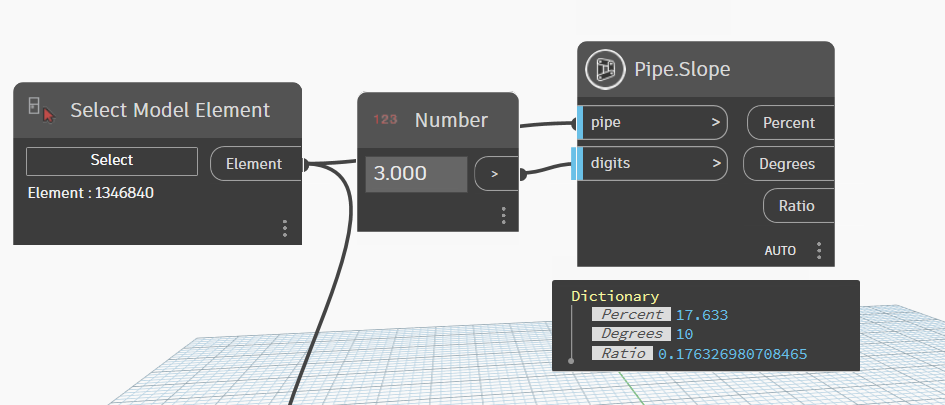
}Ta thử kiểm tra kết quả một chút
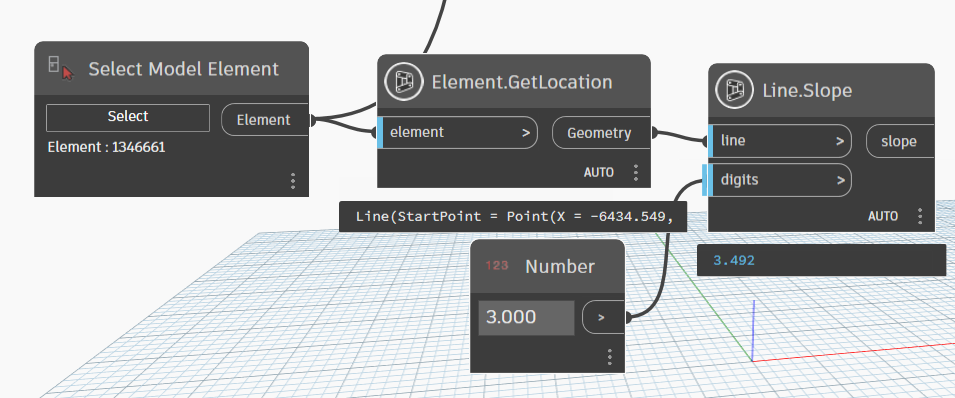
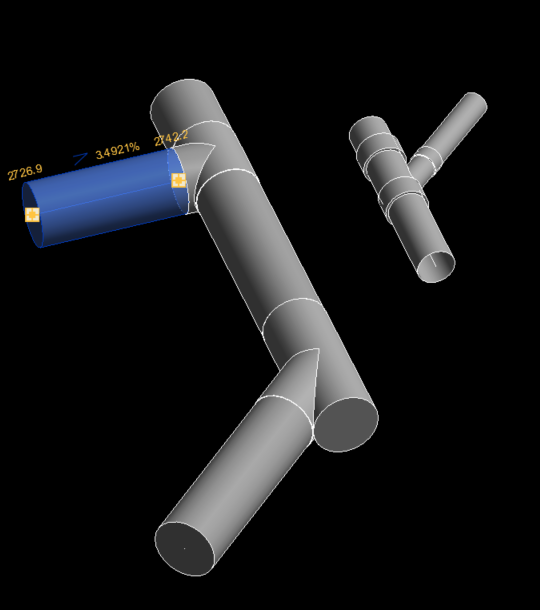
Kết quả đối chiếu với thực tế :
Mở rộng
Một số liên kết được sử dụng trong bài viết :
Mình cũng tình cờ ghé ngang qua đọc tin tức mới trên thebuildingcoder, cám ơn jeremytammik đã giành một số lời khen và gắn thẻ cho Speckle-ChuongHo-Featured Developer
Bạn đã dùng thử qua công cụ Finch chưa, có thể đây sẽ là một giải pháp tối ưu hóa thiết kế tuyệt vời trong tương lai.