Giới thiệu
Hôm nay có một người bạn gặp một vấn đề như thế này, đó là làm thế nào để tìm được đường đi ngắn nhất từ thiết bị đến thiết bị. Mình chợt nhớ ra, đúng vào năm 2017, tác giả Cesare Caoduro đã có trình bày một vấn đề gì đó tương tự như thế này và đã có một bài viết đầy đủ về nó. Vậy thì hôm nay chúng ta thử lục lọi và xem thử cách giải quyết như thế nào nhé. Tìm ra đường đi ngắn nhất là một trong những bài toán rất quan trọng, điều này áp dụng rất rộng rãi như việc bạn sử dụng Google Map giúp tìm ra đường đi từ nhà bạn đến công ty hoặc bất cứ nơi đâu.
Đặt vấn đề
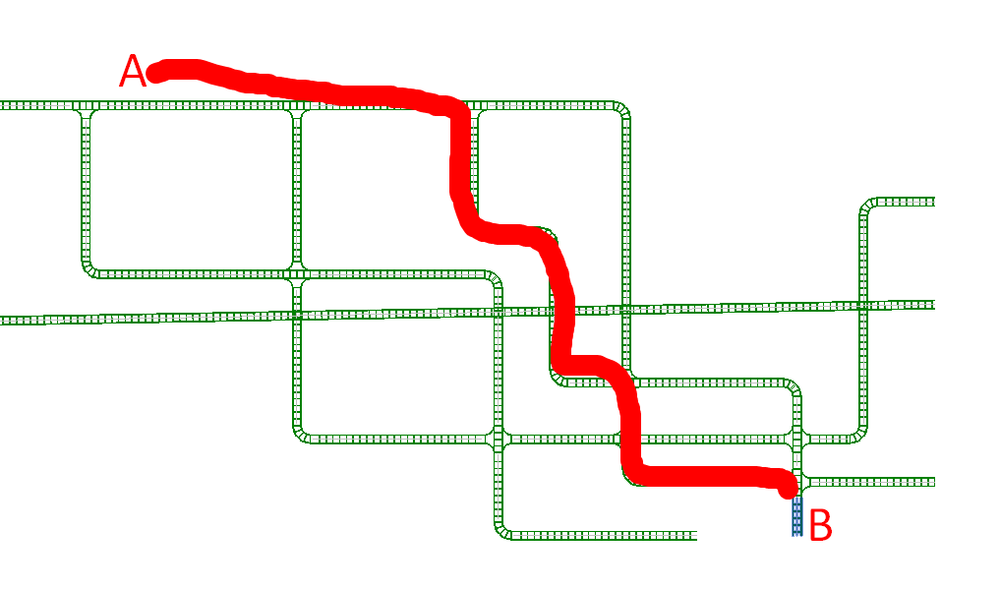
Vấn đề ở đây chính là làm sao để có thể tìm ra đường đi ngắn nhất từ một thiết bị bảng điện đến đầu còn lại của một thiết bị điện.Tại sao chúng ta phải làm điều này ?
- Giảm thiểu được tối đa đường đi chiều dài dây điện giúp tiết kiệm chi phí tối đa.
- Đưa ra đường đi tối ưu nhất trong việc tìm ra giải pháp đi dây điện tại nhiều vị trí khác nhau.
Thuật toán Dijsktra
Thuật toán Dijkstra là một trong những thuật toán cổ điển để giải quyết bài toán tìm đường đi ngắn nhất từ một điểm cho trước tới tất cả các điểm còn lại trong đồ thị có trọng số miễn là trọng số không âm.
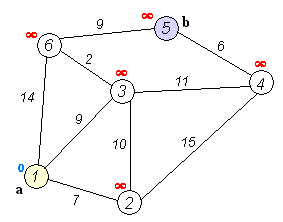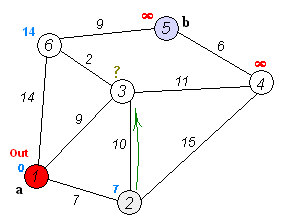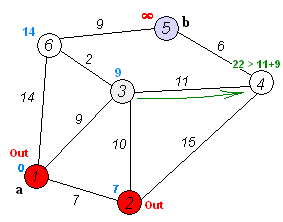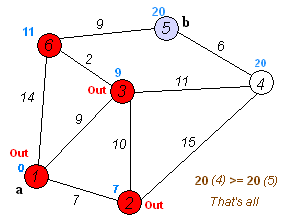
Ý tưởng cơ bản của thuật toán như sau:
Bước 1: Từ đỉnh gốc, khởi tạo khoảng cách tới chính nó là 0, khởi tạo khoảng cách nhỏ nhất ban đầu tới các đỉnh khác là vô cùng. Ta được danh sách các khoảng cách tới các đỉnh.
Bước 2: Chọn đỉnh A có khoảng cách nhỏ nhất trong danh sách này và ghi nhận. Các lần sau sẽ không xét tới đỉnh này nữa.
Bước 3: Lần lượt xét các đỉnh kề B của đỉnh A. Nếu khoảng cách từ đỉnh gốc tới đỉnh B nhỏ hơn khoảng cách hiện tại đang được ghi nhận thì cập nhật giá trị và đỉnh kề A vào khoảng cách hiện tại của B.
Bước 4: Sau khi xét tất cả đỉnh kề B của đỉnh A. Lúc này ta được danh sách khoảng cách tới các điểm đã được cập nhật. Quay lại Bước 2 với danh sách này. Thuật toán kết thúc khi chọn được khoảng cách nhỏ nhất từ tất cả các điểm.
Để dễ dàng hiểu ý tưởng của thuật toán. Chúng ta cùng xem ví dụ với đồ thị vô hướng GGG. Thuật toán Dijkstra sẽ tìm khoảng cách từ đỉnh gốc 0 tới tất cả các đỉnh còn lại trong đồ thị G.
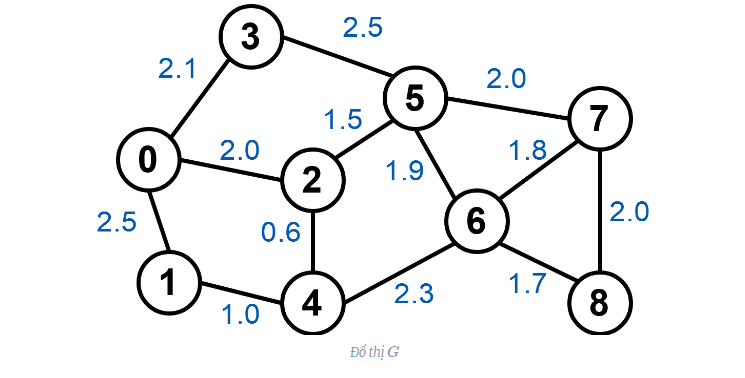
Đầu tiên, khởi tạo khoảng cách nhỏ nhất ban đầu tới các đỉnh khác là +∞ và khoảng cách tới đỉnh gốc là 0. Ta được danh sách các khoảng cách tới các đỉnh.
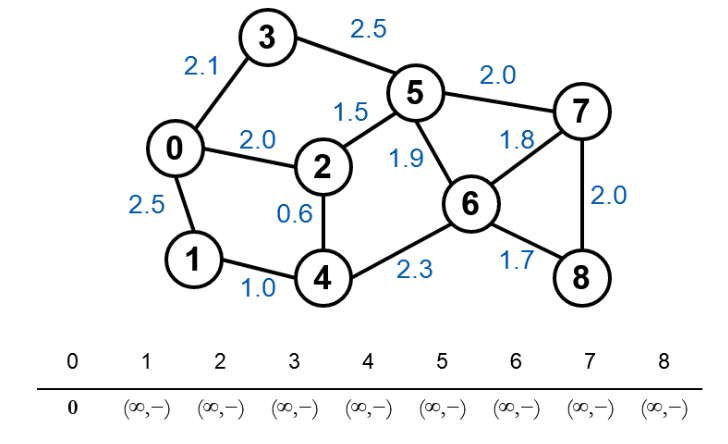
Chọn đỉnh 0 có giá trị nhỏ nhất, xét các đỉnh kề của đỉnh 0: Xét đỉnh 1, khoảng cách từ gốc đến đỉnh 1 là 2.5 < +∞ nên ghi nhận giá trị mới là (2.5,0)(2.5, 0)(2.5,0) (nghĩa là khoảng cách đến đỉnh gốc hiện tại ghi nhận là 2.5, đỉnh kề liền trước là đỉnh 0). Xét tương tự cho đỉnh 2 và 3, ta được dòng thứ 2 trong bảng.
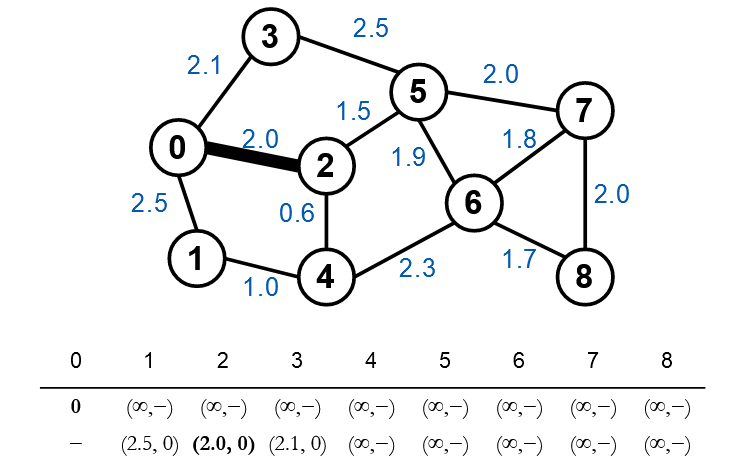
Sau khi xét tất cả các đỉnh ta chọn đỉnh 2 có khoảng cách nhỏ nhất và ghi nhận để xét tiếp. Tiếp tục xét đỉnh kề của 2 là đỉnh 4 và 5 với nguyên tắc nêu ở trên. Xét đỉnh 4, khoảng cách từ đỉnh gốc đến đỉnh 4 sẽ bằng khoảng cách từ đỉnh gốc tới đỉnh 2 cộng khoảng cách từ 2 đến 4. Nghĩa là 2.0+0.6=2.62.0+0.6=2.62.0+0.6=2.6 nên ta ghi nhận khoảng cách tại đỉnh 4 là (2.6,2)(2.6, 2)(2.6,2). Xét tương tự cho đỉnh 5.
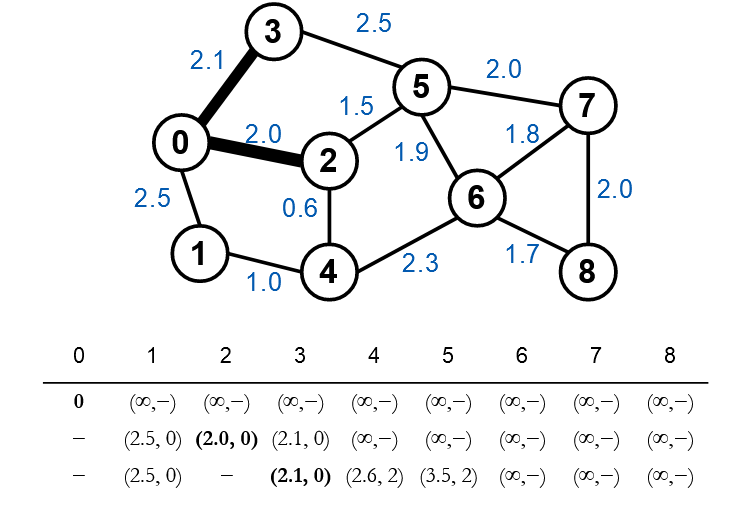
Lúc này ta chọn được đỉnh 3 có khoảng cách nhỏ nhất, xét đỉnh kề của đỉnh 3 là đỉnh 5. Khoảng cách từ gốc tới đỉnh 5 =2.1+2.5=4.6=2.1+2.5=4.6=2.1+2.5=4.6 lớn hơn khoảng cách hiện tại được ghi nhận, vì vậy giá trị tại đỉnh 5 không đổi.
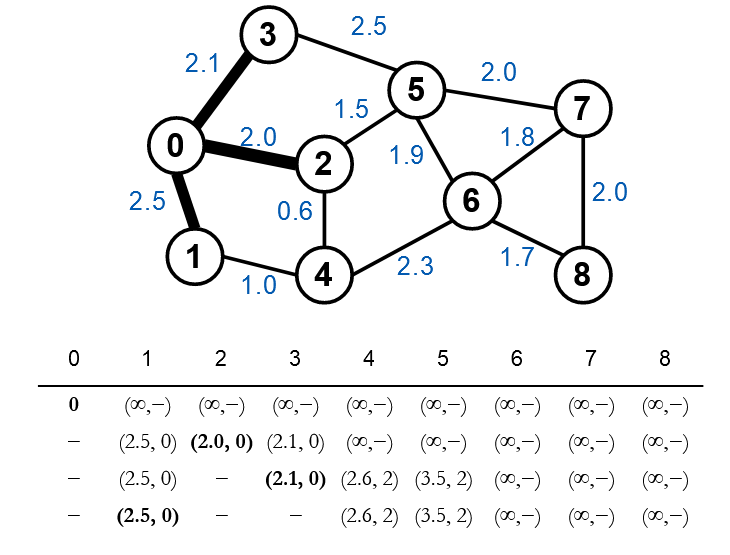
Đỉnh 1 là đỉnh được chọn tiếp theo, xét đỉnh kề của 1 là đỉnh 4. Khoảng cách từ đỉnh gốc không nhỏ hơn khoảng cách hiện tại nên ta không cập nhật gì ở đỉnh này.
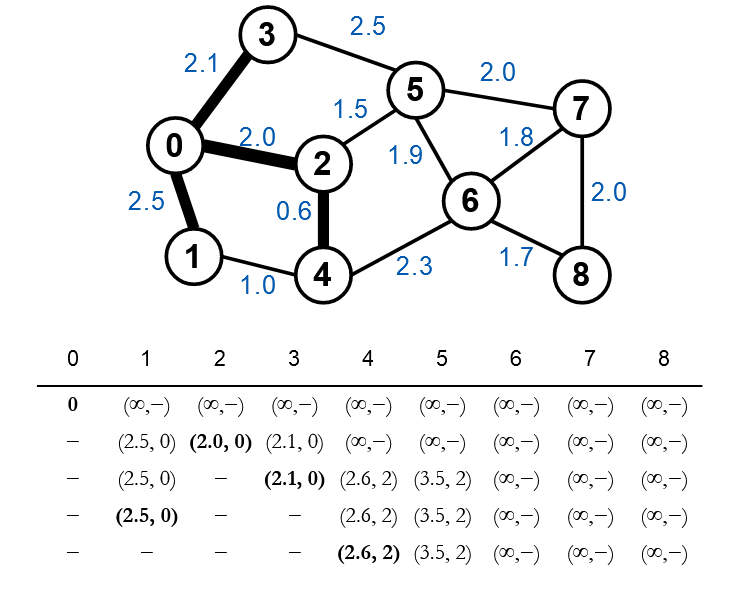
Sau khi xét xong ta chọn được đỉnh 4 là đỉnh tiếp theo. Ta cập nhật giá trị mới cho đỉnh 6.
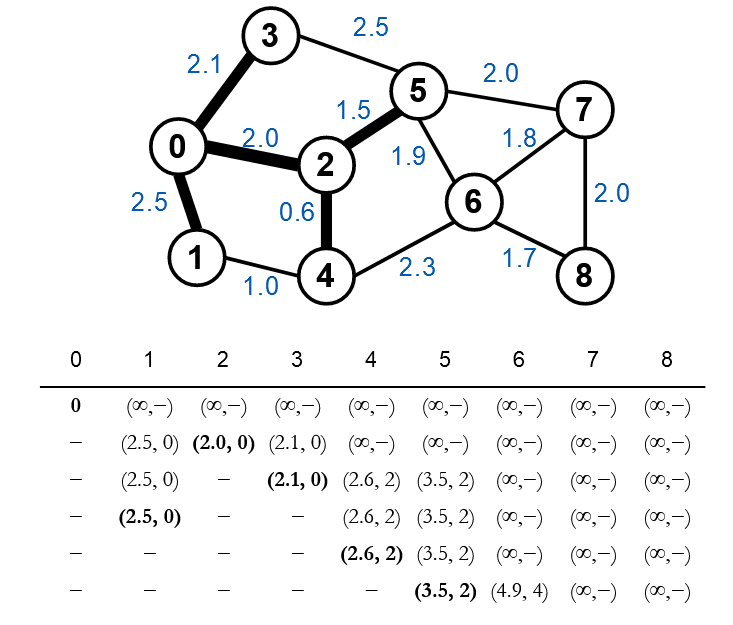
Chọn được đỉnh 5 là đỉnh nhỏ nhất, tiếp tục xét các đỉnh kề.
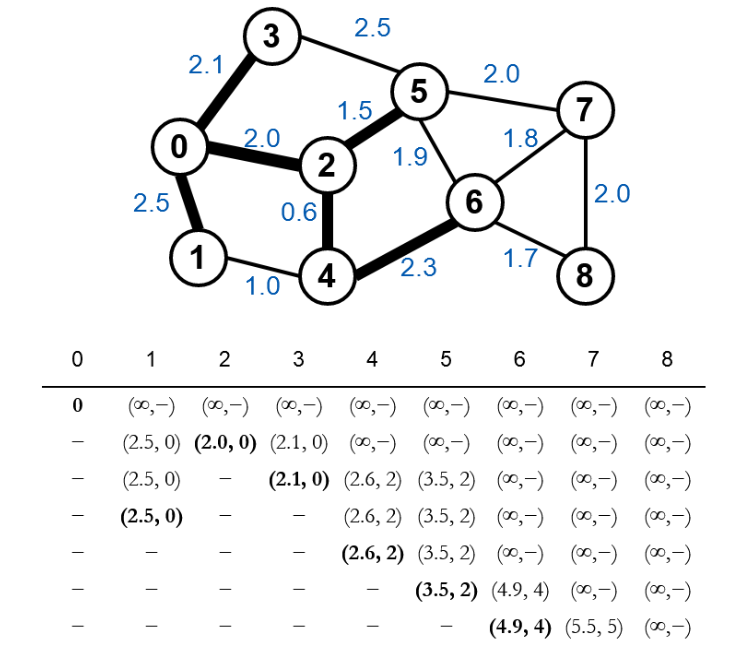
Đỉnh 6 là đỉnh tiếp theo được chọn.
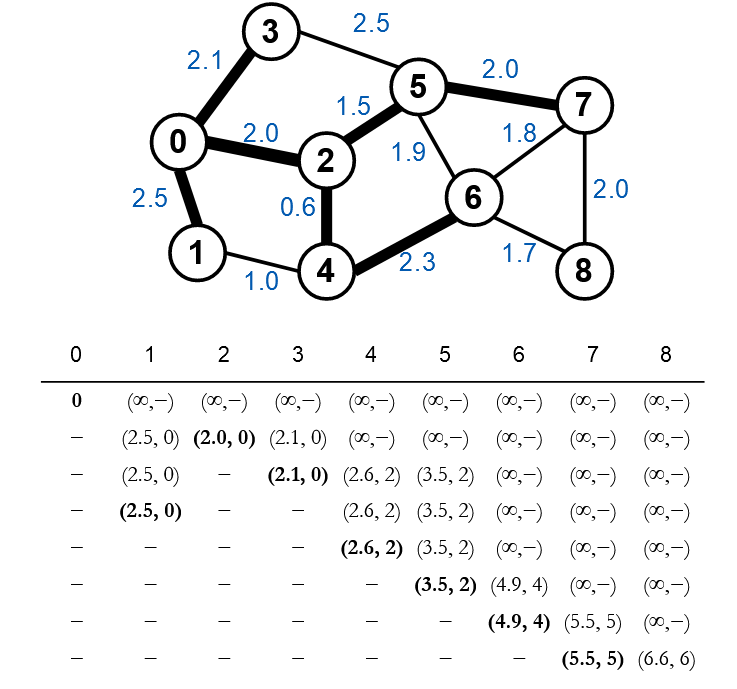
Chọn đỉnh có khoảng cách nhỏ nhất là đỉnh 7.
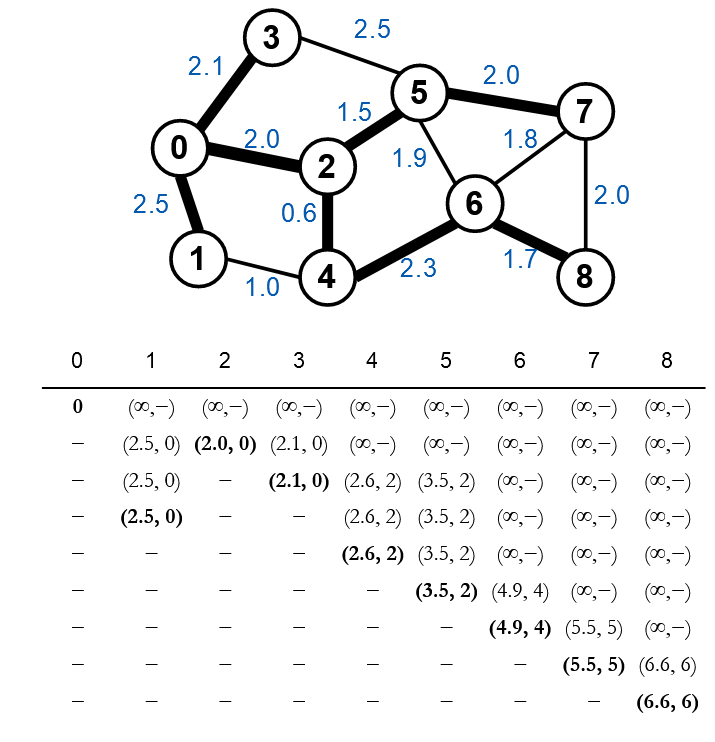
Thuật toán kết thúc khi chọn được khoảng cách nhỏ nhất cho tất cả các đỉnh.
Xử lý vấn đề
Nói về xử lý vấn đề với lý thuyết bên trên, chắc chắn nhiều người sẽ hoài nghi và không có cách nào hiểu cho đến khi áp dụng vào một bài toán thực tế. Điều đầu tiên chính là xác định việc tìm ra các kết nối giữa đổi tượng này và đối tượng kia, ở đây chính là toàn bộ các đối tượng kết nối (ref) chưa xử lý. Để làm được điều này, bạn cần lấy về các connector và lấy về toàn bộ ref giữa chúng, chính xác ref sẽ là cách để ta tìm ra đối tượng liên kết chính xác tiếp theo của đường đi một máng điện, trong bài toán này các ref chính là lấy từ hai Categories Cable Tray và Cable Tray Fittings.
# Copyright Cesare Caoduro 2017
# Mail: cesare.caoduro@gmail.com
# Twitter: @CesareCaoduro
import clr
import math
clr.AddReference("RevitServices")
import RevitServices
from RevitServices.Persistence import DocumentManager
from RevitServices.Transactions import TransactionManager
doc = DocumentManager.Instance.CurrentDBDocument
clr.AddReference("RevitAPI")
import Autodesk
from Autodesk.Revit.DB import *
clr.AddReference("RevitNodes")
import Revit
clr.ImportExtensions(Revit.Elements)
clr.ImportExtensions(Revit.GeometryConversion)
clr.AddReference('DSCoreNodes')
from DSCore import *
#The inputs to this node will be stored as a list in the IN variables.
if isinstance(IN[0], list):
elements = UnwrapElement(IN[0])
toggle = 0
else:
toggle = 1
elements = [UnwrapElement(IN[0])]
p = []
dir = []
rep = []
ref = []
elements = List.Flatten(elements,2)
for e in elements:
refs = []
try:
connectors = e.MEPModel.ConnectorManager.Connectors
except:
connectors = e.ConnectorManager.Connectors
for conn in connectors:
for c in conn.AllRefs:
refs.append(c.Owner)
ref.append(refs)
#Assign your output to the OUT variable.
if toggle:
OUT = refs
else:
OUT = ref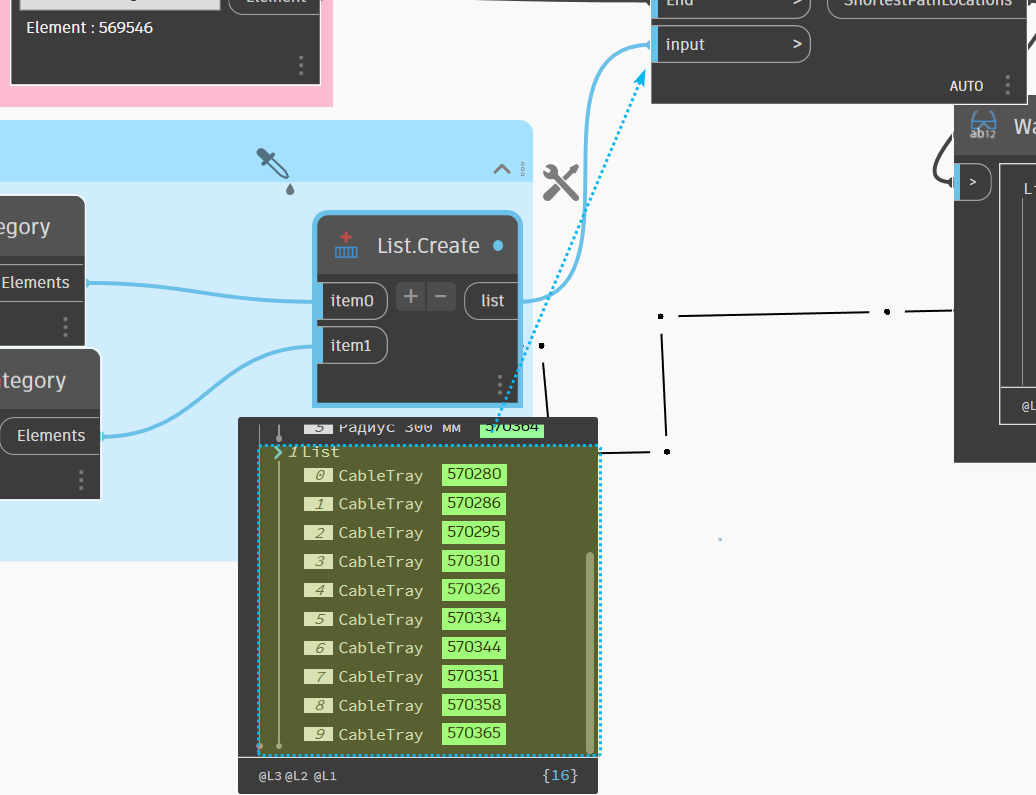
Công việc tiếp theo chính là làm sao để lấy về được đối tượng nào gần nhất để đặt kết nối và là điểm xuất phát trong đồ thị. Đó là bước nhảy A như đã giải thích ở thuật toán bên trên. Kết quả trả về chính là hai Cable Tray gần nhất so với hai đối tượng được chọn. Việc tìm ra cũng khá dễ dàng , đó là sử dụng cách tính khoảng cách giữa hai điểm. Trong không gian Oxyz khoảng cách giữa hai điểm được tính bằng việc bình phương khoảng cách và tính căn bậc hai vì vậy ta viết trước hai hàm tính cân bậc hai là pow2 và hàm tính về khoảng cách distance. Duyệt qua các điểm đã tính để tìm ra điểm gần nhất. Và cũng do CableTray là đối tượng trả về đoạn Line không phải một điểm như Calbe Tray Fittings nên cũng cần phải so sánh đến hai điểm để xem điểm nào gần nhất chứ không phải một điểm. Hàm Curve.PointAtParameter(eLoc,0) sẽ là cách để tìm ra điểm đầu của Cable Tray và thay trọng số là một tương tự cho việc tìm điểm cuối.
# Copyright Cesare Caoduro 2017
# Mail: cesare.caoduro@gmail.com
# Twitter: @CesareCaoduro
import clr
import math
clr.AddReference('ProtoGeometry')
from Autodesk.DesignScript.Geometry import *
clr.AddReference('DSCoreNodes')
from DSCore import *
def pow2(n):
return math.pow(n,2)
def distance(p1,p2):
return math.fabs(math.sqrt(pow2(p2.X-p1.X)+pow2(p2.Y-p1.Y)+pow2(p2.Z-p1.Z)))
#The inputs to this node will be stored as a list in the IN variables.
elements = List.Flatten(IN[0],2)
start = IN[1]
startLoc = start.GetLocation()
end = IN[2]
endLoc = end.GetLocation()
points = []
pointElements = []
for e in elements:
eLoc = e.GetLocation()
#startEndPoint.append(eLoc)
try:
s1 = Curve.PointAtParameter(eLoc,0)
points.append(s1)
pointElements.append(e)
s2 = Curve.PointAtParameter(eLoc,1)
points.append(s2)
pointElements.append(e)
except:
points.append(eLoc)
pointElements.append(e)
d0S = 1000000000
d0E = 1000000000
minS, minE = [],[]
sEl, eEl = [],[]
for p,e in zip(points,pointElements):
dS = distance(p,startLoc)
dE = distance(p,endLoc)
if (dS<d0S):
minS = p
sEl = e
d0S = dS
if (dE<d0E):
minE = p
eEl = e
d0E = dE
OUT = sEl,eEl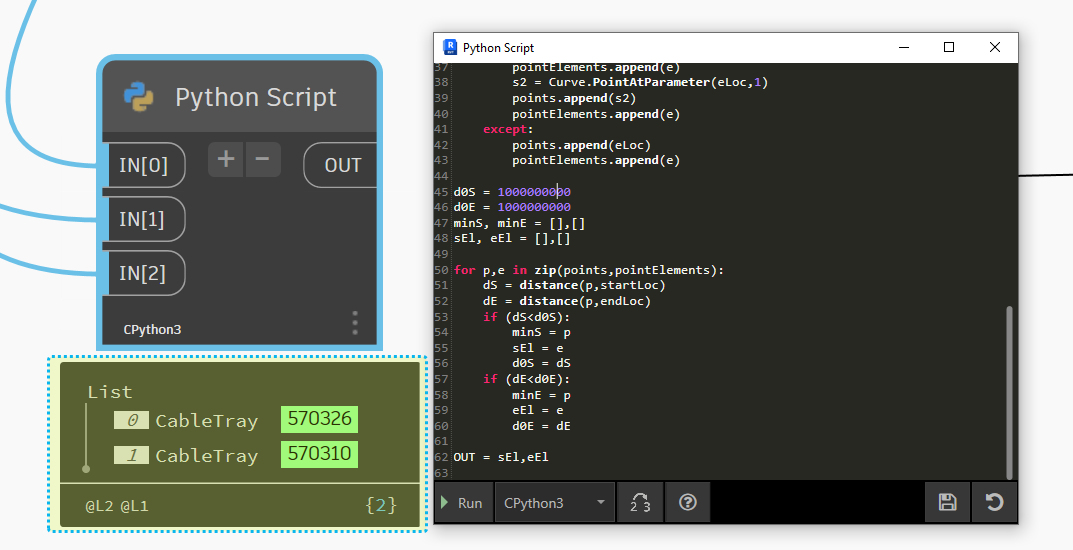
Sau khi có được các đối tượng để lấy nút thì điều cần làm bây giờ chính là xác định từng cặp kết nối để tạo ra đồ thị.
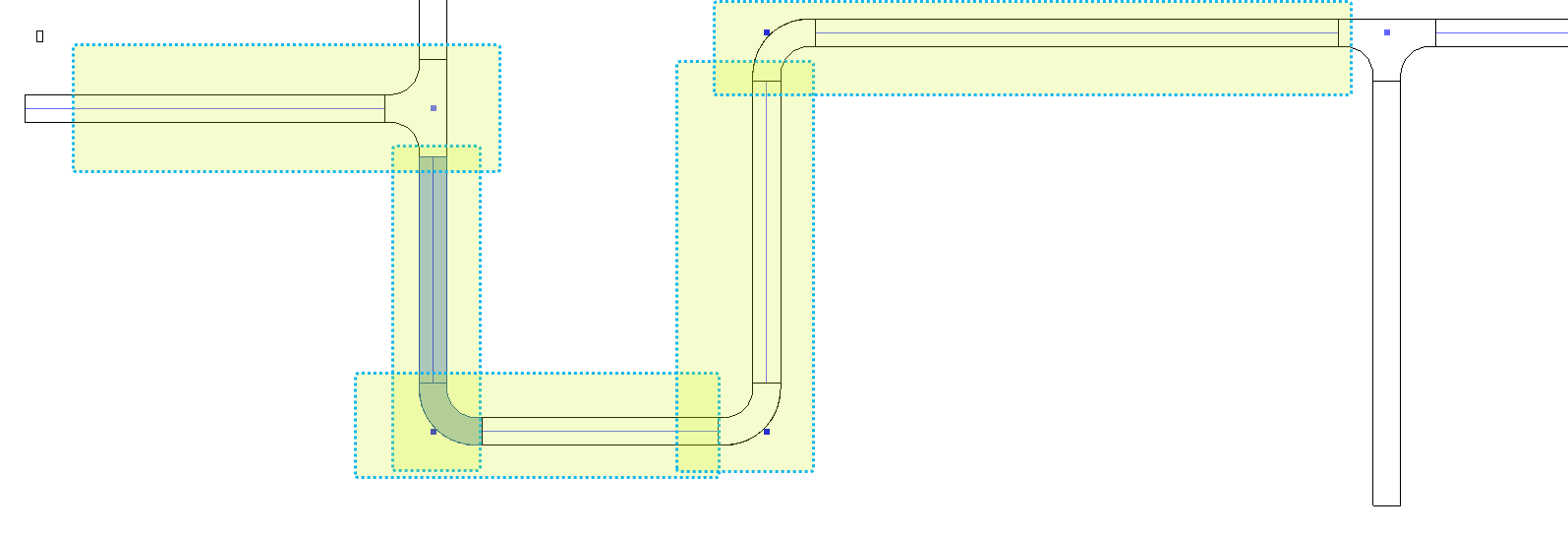
Tổng hợp các thông tin ở trên, bây giờ bạn đang có : Đối tượng đầu tiên của đường đi ngắn nhất so với điểm đầu, đối tượng kết thúc của đường gần nhất so với điểm cuối, và một danh sách cặp kết nối để giúp định hình đường đi để tìm ra mối liên hệ giữa hai điểm đầu cuối.
Vậy bây giờ ta sẽ áp dụng thuật toán dijsktra như đã trình bày để tìm ra đường đi ngắn nhất trên máng điện.Ở đây tác giả tạo ra một lớp là Graph() để định hình với edges là danh sách của tất cả các nút tiếp theo có thể, weights là danh sách trọng số (Khoảng cách) giữa hai nút.Tức nghĩa ở đây là tác giả đang muốn tạo ra một Graph bao gồm dữ liệu quan trọng nhất đó chính là cặp kết nối giữa các nút và khoảng cách trọng số để giải thuật.
class Graph():
def __init__(self):
"""
self.edges is a dict of all possible next nodes
e.g. {'X': ['A', 'B', 'C', 'E'], ...}
self.weights has all the weights between two nodes,
with the two nodes as a tuple as the key
e.g. {('X', 'A'): 7, ('X', 'B'): 2, ...}
"""
self.edges = defaultdict(list)
self.weights = {}
def add_edge(self, from_node, to_node, weight):
# Note: assumes edges are bi-directional
self.edges[from_node].append(to_node)
self.edges[to_node].append(from_node)
self.weights[(from_node, to_node)] = weight
self.weights[(to_node, from_node)] = weightVà như cách đã trình bày về thuật toán dijsktra đã trình bày bên trên, chúng ta sẽ khởi tạo đường đi ngắn nhất là 0 và bắt đầu tìm ra khoảng cách liền kề của A, ở đây A chính là điểm xuất phát của Cable Tray và với mỗi lần duyệt qua như vậy ta sẽ ghi lại trọng số khoảng cách để tìm ra nút tiếp theo và cộng dồn trọng số để tiếp tục so sánh khoảng cách các nút. Và cứ thế cho đến hết chính là điểm cuối của đối tượng.Kết quả cuối cùng sẽ là đường đi bao gồm các ilne của Cable Tray và điểm chính là điểm của mỗi Cable Tray Fitting.Tổng hợp lại mỗi bước đi ta có mảng danh sách trả về là đường đi từ điểm đầu đến điểm cuối đối tượng.
import clr
clr.AddReference('ProtoGeometry')
from Autodesk.DesignScript.Geometry import *
import sys
sys.path.append(r'C:\Program Files (x86)\IronPython 2.7\Lib')
# Import RevitAPI
clr.AddReference("RevitAPI")
import Autodesk
from Autodesk.Revit.DB import *
# Import ToDSType(bool) extension method
clr.AddReference("RevitNodes")
import Revit
clr.ImportExtensions(Revit.Elements)
from collections import defaultdict
class Graph():
def __init__(self):
"""
self.edges is a dict of all possible next nodes
e.g. {'X': ['A', 'B', 'C', 'E'], ...}
self.weights has all the weights between two nodes,
with the two nodes as a tuple as the key
e.g. {('X', 'A'): 7, ('X', 'B'): 2, ...}
"""
self.edges = defaultdict(list)
self.weights = {}
def add_edge(self, from_node, to_node, weight):
# Note: assumes edges are bi-directional
self.edges[from_node].append(to_node)
self.edges[to_node].append(from_node)
self.weights[(from_node, to_node)] = weight
self.weights[(to_node, from_node)] = weight
def dijsktra(graph, initial, end):
# shortest paths is a dict of nodes
# whose value is a tuple of (previous node, weight)
shortest_paths = {initial: (None, 0)}
current_node = initial
visited = set()
while current_node != end:
visited.add(current_node)
destinations = graph.edges[current_node]
weight_to_current_node = shortest_paths[current_node][1]
for next_node in destinations:
weight = graph.weights[(current_node, next_node)] + weight_to_current_node
if next_node not in shortest_paths:
shortest_paths[next_node] = (current_node, weight)
else:
current_shortest_weight = shortest_paths[next_node][1]
if current_shortest_weight > weight:
shortest_paths[next_node] = (current_node, weight)
next_destinations = {node: shortest_paths[node] for node in shortest_paths if node not in visited}
if not next_destinations:
return "Route Not Possible"
# next node is the destination with the lowest weight
current_node = min(next_destinations, key=lambda k: next_destinations[k][1])
# Work back through destinations in shortest path
path = []
while current_node is not None:
path.append(current_node)
next_node = shortest_paths[current_node][0]
current_node = next_node
# Reverse path
path = path[::-1]
return path
start = IN[0]
end = IN[1]
edges = IN[2]
graph = Graph()
for edge in edges:
graph.add_edge(edge[0],edge[1],1)
#Assign your output to the OUT variable.
OUT = dijsktra(graph, start, end)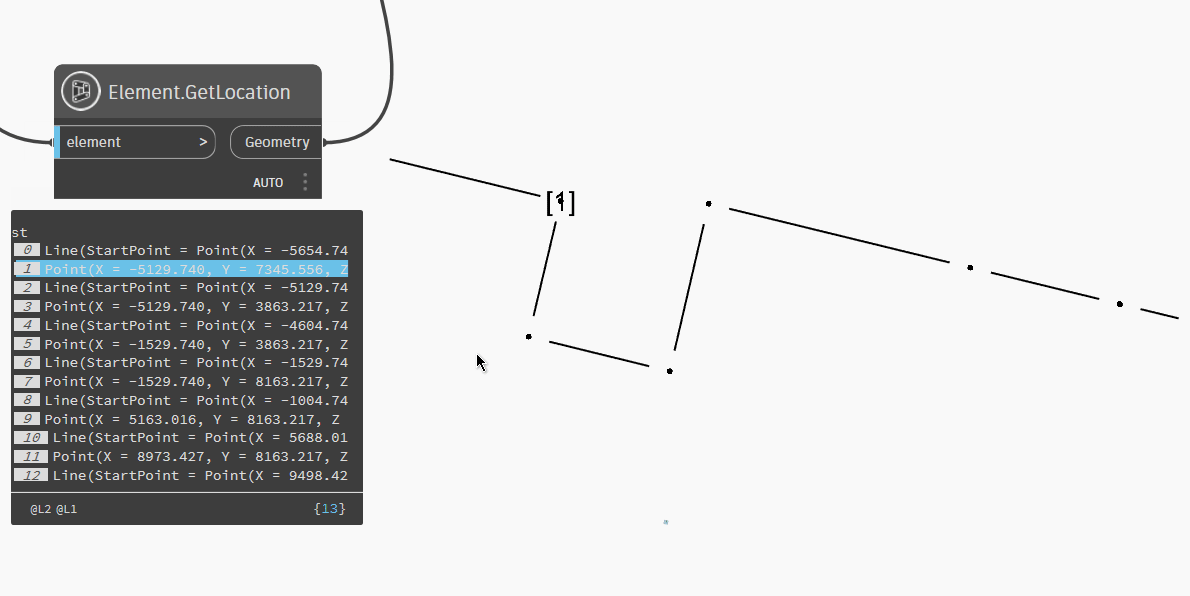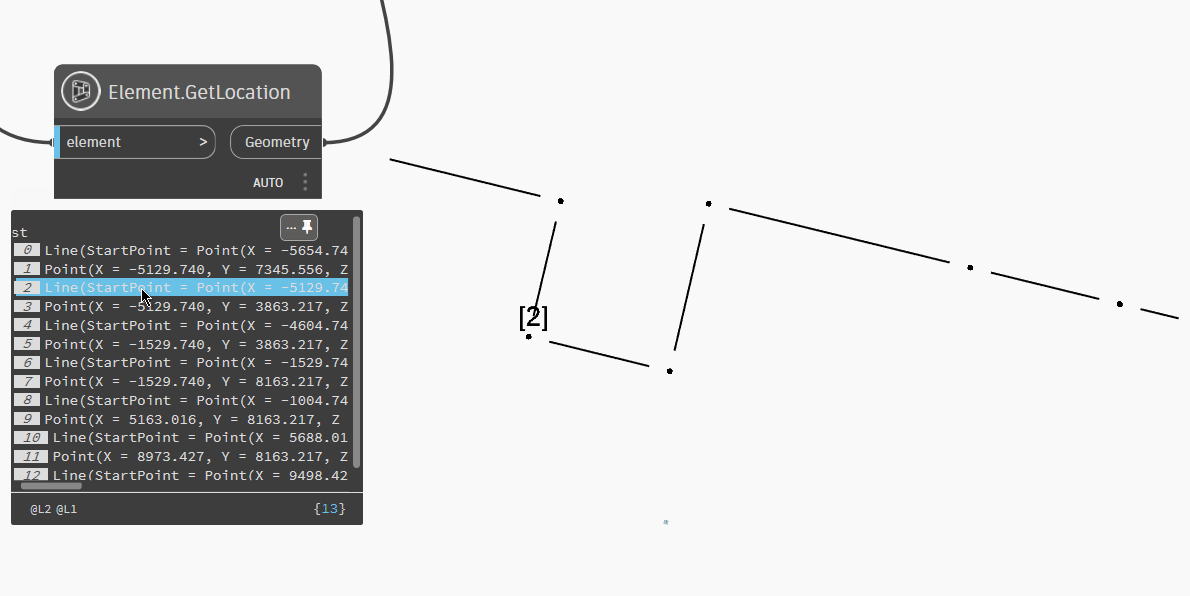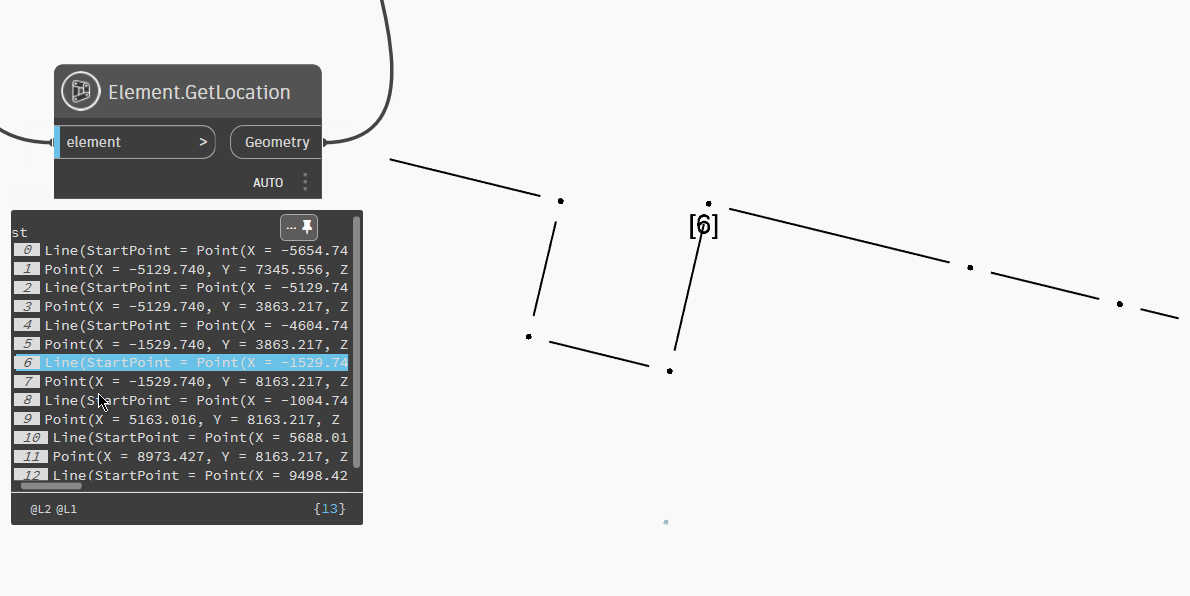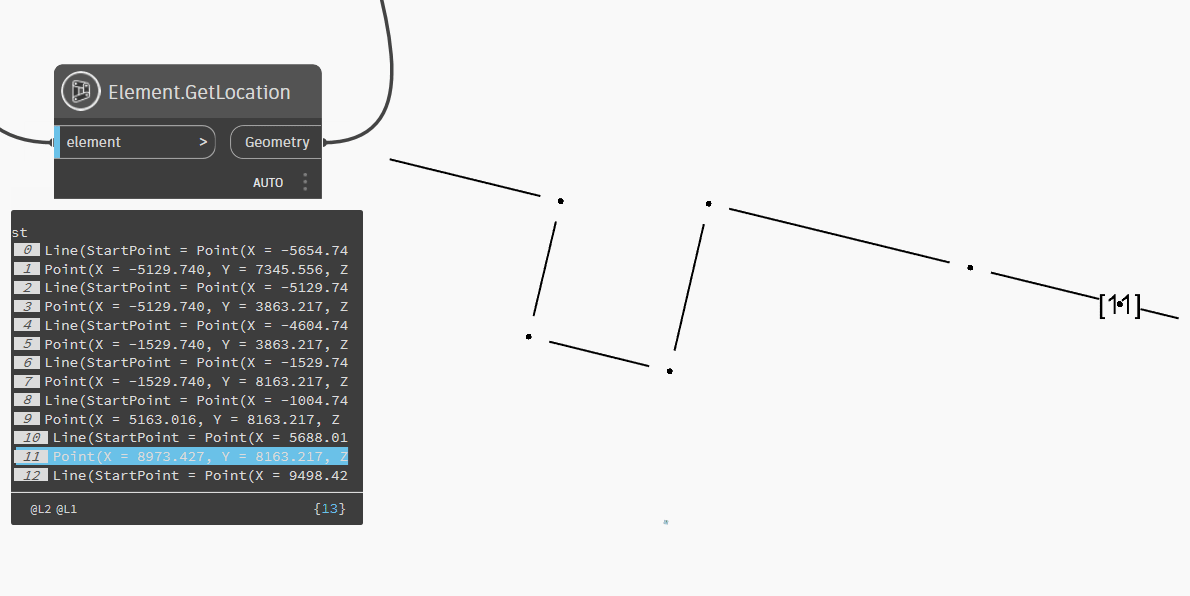
Cuối cùng chúng ta sẽ build một script để dễ dàng thực hiện ý tưởng này. Đầu vào sẽ yêu cầu một số thông tin sau :
Bước 1: Select Model Element : Chọn thiết bị đầu vào 1 (Để lấy điểm đầu đối tượng).
Bước 2: Select Model Element : Chọn thiết bị đầu ra 2 (Để lấy điểm cuối đối tượng).
Bước 3: Categories : Chọn Categories CableTray, tức là element để định hình đường đi của máng điện.
Bước 4: Categories : Chọn Categories CableTray Fittings, tức là các albow,cross đi kèm để thêm vào định hình đường đi của toàn bộ liên kết máng điện.
Đầu ra mong muốn sẽ là đường đi và toàn bộ đối tượng biểu diễn cho đường đi của máng điện.Với việc này bạn có thể dễ dàng tính toán được sẽ sử dụng bao nhiêu mét dây điện để chi phí là tiết kiệm nhất. Tất nhiên với bài toán tối ưu cả về mặt đường đi lẫn chi phí sẽ là giai đoạn sau của bài toán này.
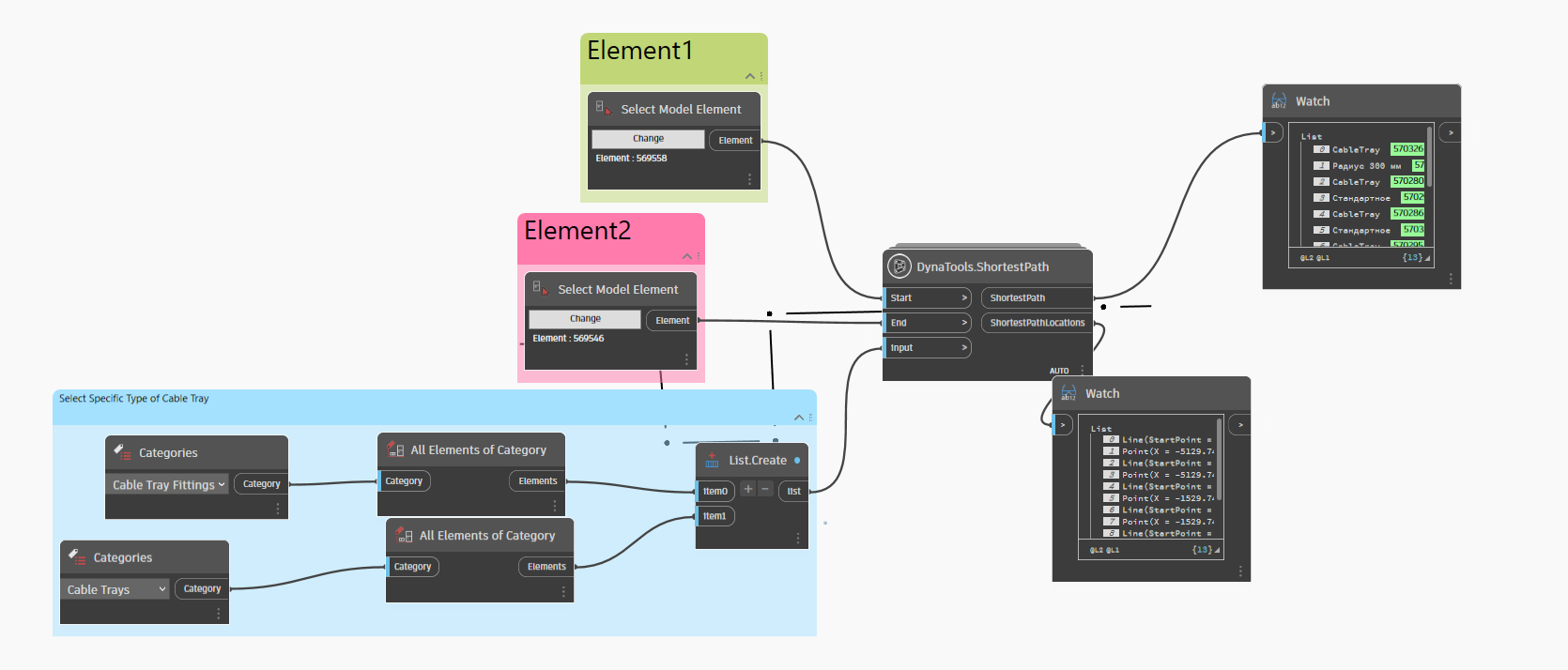
Bạn có thể xem qua kết quả diễn giải bên dưới, khi chọn hai đối tượng và thay đổi vị trí đối tượng đi một vị trí mới, đường đi màu xanh biểu thị cho đường đi ngắn nhất từ thiết bị này đến thiết bị khác. Ở đây mình sẽ thử thay đổi vị trí của cả hai thiết bị để xem liệu đường đi ngắn nhất có bị thay đổi không.
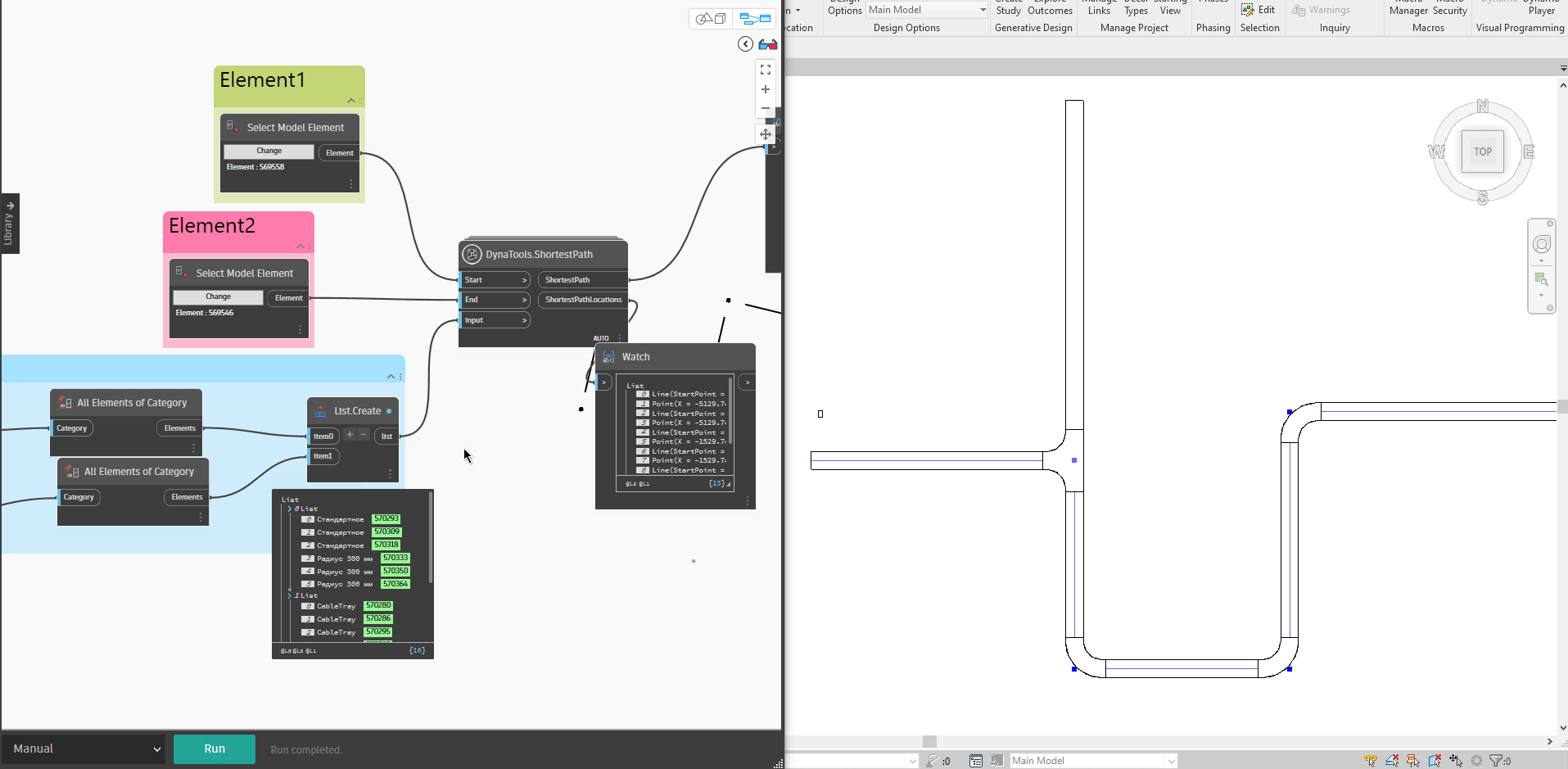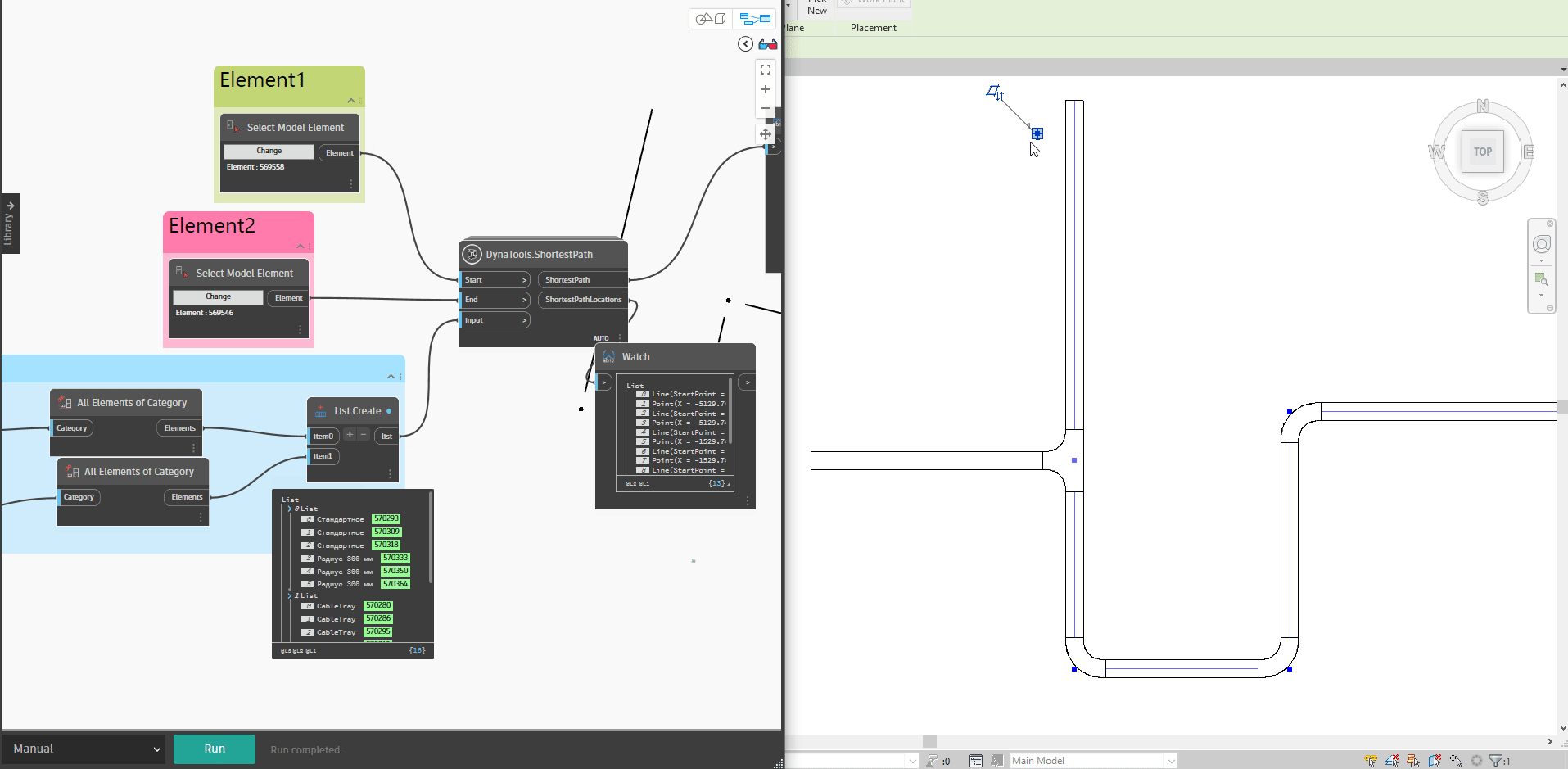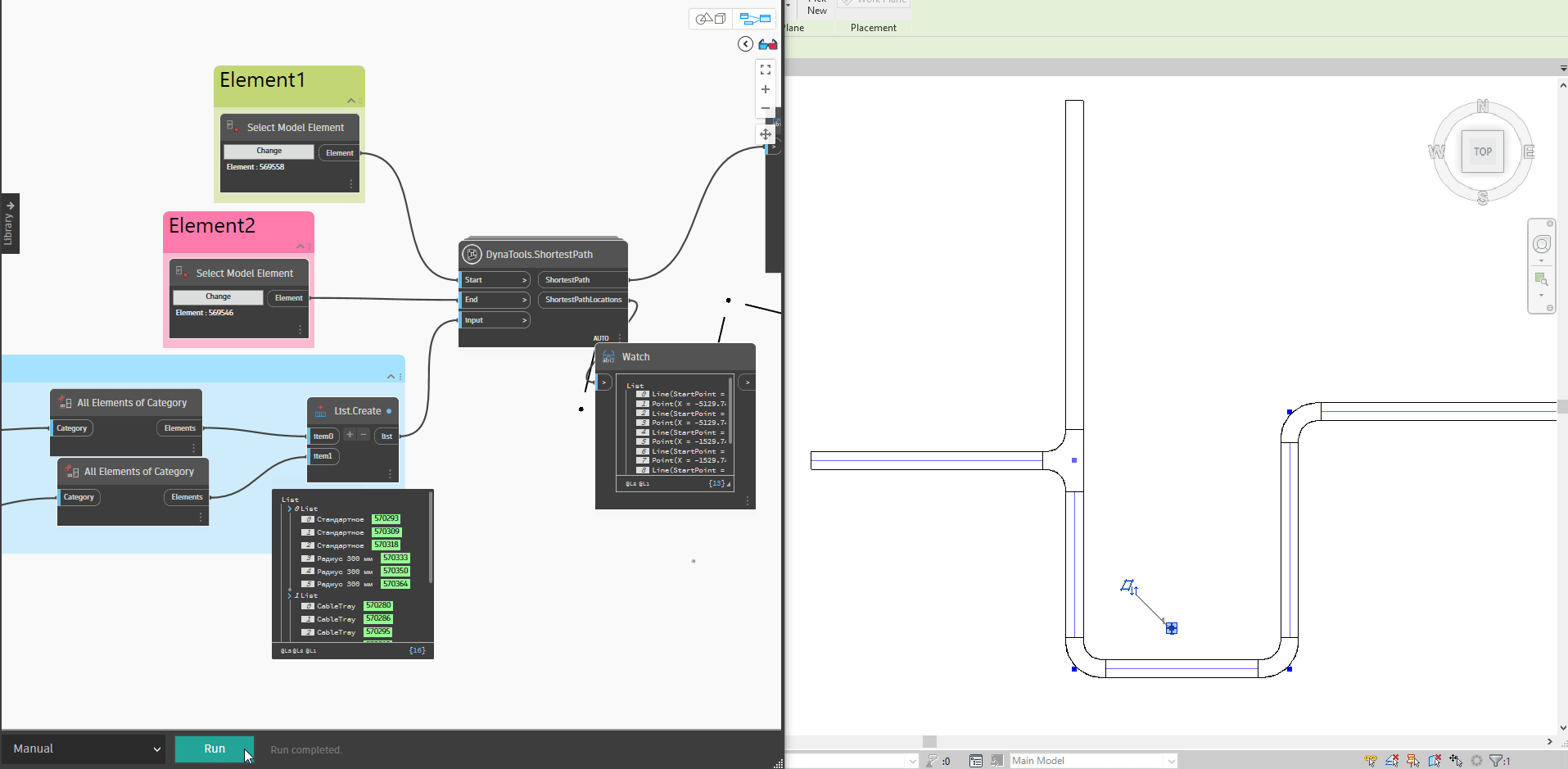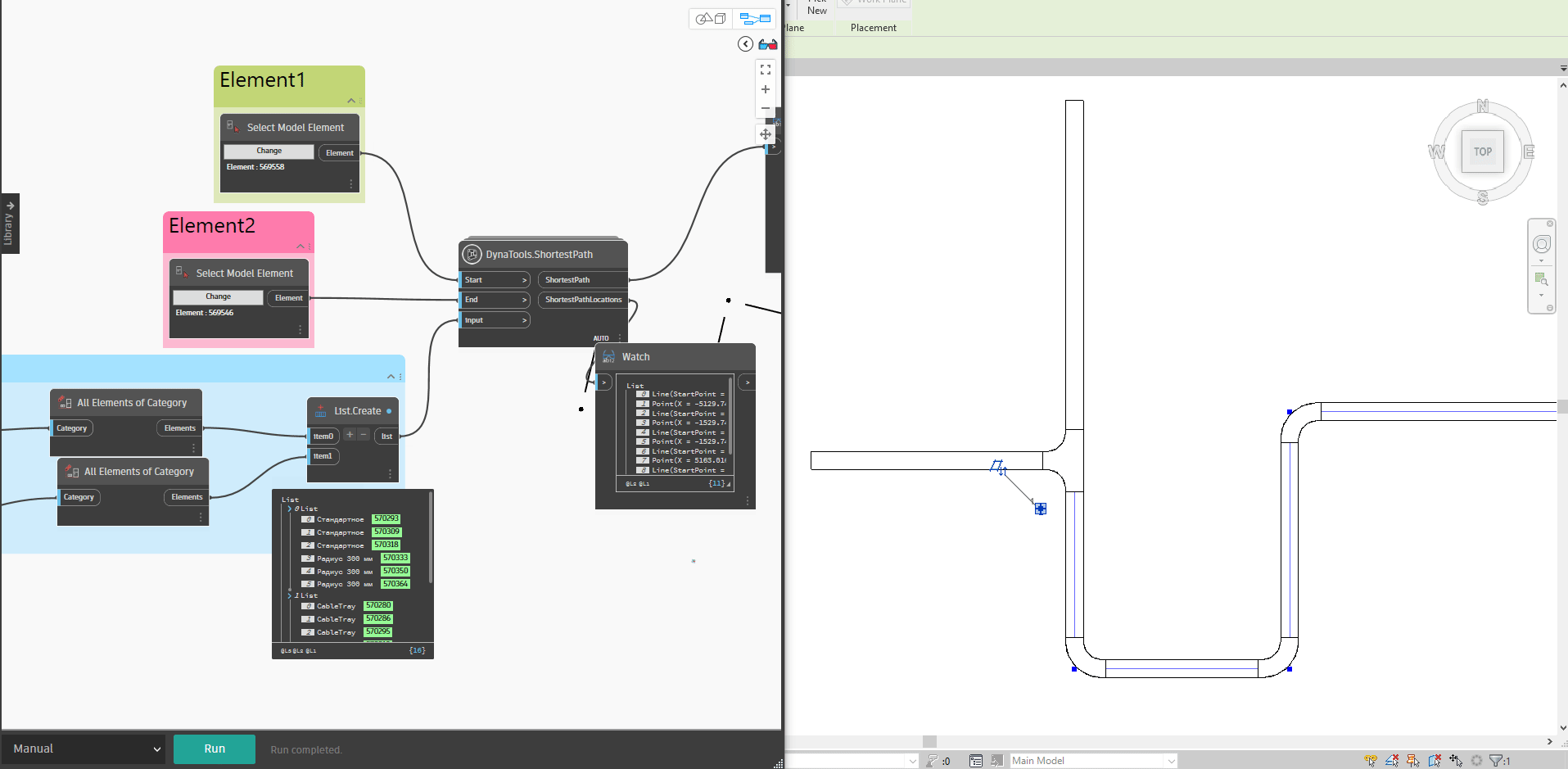
Rõ ràng với các kết quả bên trên, chính là những điều mà chúng ta đang muốn tìm ra phải không nào. Scripts này được mình chia sẻ và bạn có thể tải về tại đây để nghiên cứu :
Mở rộng
Tất nhiên với kiến thức trình bày lại của mình cũng không thể nào bao quát hết những ý mà tác giả muốn truyền đạt vì tính nhất quán của mã. Vì vậy với cách trình bày trên chỉ giúp bạn hiểu các vận hành và tạo ra một node để sử dụng và mang mục đích tham khảo. Nếu bạn muốn tìm hiểu sâu hơn hãy xem xét từ bài MEP Modeling Made Easy with Dynamo của tác giả Cesare Caoduro. Trước đây mình cũng đã có một bài chia sẻ về cách tìm đường ngắn nhất của điểm qua genetic algorithm và chúng vẫn còn ở liên kết Create Cloosed Loop of Lines By points , bạn có thể tự tìm hiểu thêm.
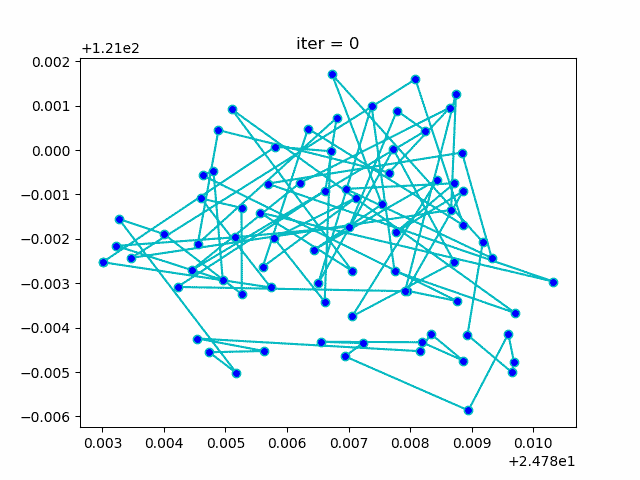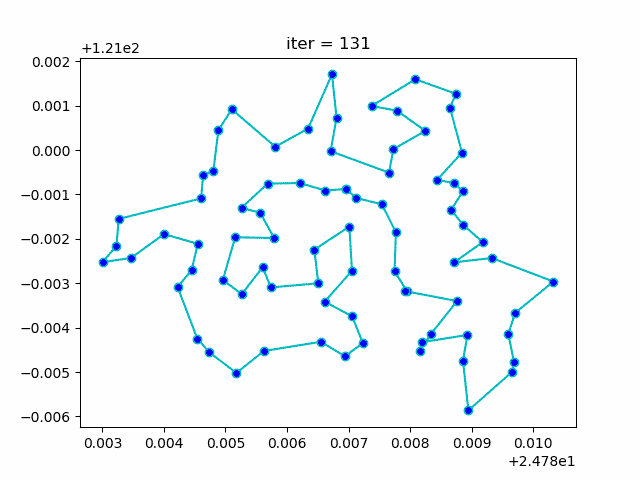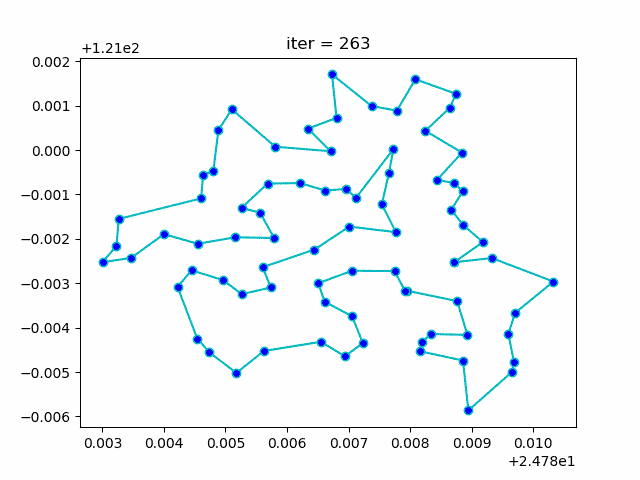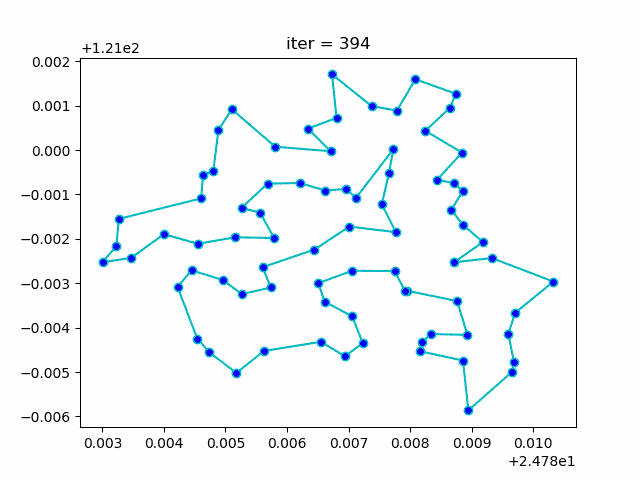
Kết quả của bài toán này cũng rất ấn tượng.