Mở đầu
Ở trường đại học, chúng ta đã học rất nhiều về toán ma trận, nhưng lại rất ít áp dụng, hầu như mọi người đều lãng quên nó sau khi rời bỏ ngôi trường yêu quý của mình. Có người nói với mình rằng, nó vô dụng và hầu như chả giúp ích gì cho họ cả.Hôm nay mình sẽ cùng các bạn tản mạn một xíu.Tại sao chúng ta lại được học toán ma trận và liệu học toán ma trận có giúp ích gì cho chúng ta hay không?
Ma trận cơ bản
Một tập hợp toán ma trận gồm mộ nhóm theo cột và hàng theo hình chữ nhật, bên trong là các phần tử ứng mỗi vị trí gióng theo hàng và cột.Các ma trận có thể được hoán đổi hoặc nhân với nhau và cho ra một kết quả khác của ma trận.

Ví dụ trên chính là một ma trận mxn, các hàng m nằm ngang và n cột theo chiều dọc.Mỗi phần tử của một ma trận thường được biểu thị bằng một biến ví dụ như a21 đại diện cho phần tử ở hàng thứ hai và cột thứ 1 của ma trận.
Trò chơi kéo búa bao
Biết lý thuyết sơ sơ vậy để mình thử với bài toán kéo búa bao này như thế nào nhé.
Bây giờ mình sẽ tạo ra một trò chơi nho nhỏ để chơi với máy và quy ước như sau:
- Kéo thắng bao
- Bao thắng búa
- Búa thắng kéo
Viết một chương trình máy tính để mô phỏng lại trò chơi này.Mình sẽ tạo ra một con máy giả để chơi oẳn tù tì với mình.
Giờ mình sẽ mô phỏng lại các lượt thắng thua trên một bảng giữa người và máy xem như nào.
Ví dụ :
Máy : Bao | Tôi : Bao
Kết quả : Hoà
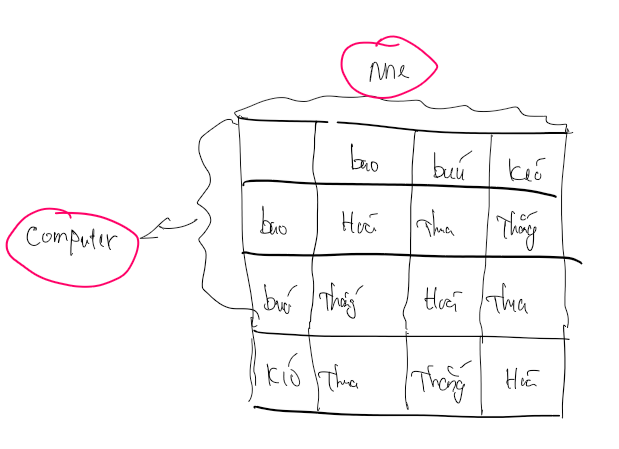
Kết quả cuối cùng ta sẽ có được bảng biểu diễn như bên trên.
Mọi ý tưởng ban đầu đã xong xuôi, giờ nhìn có vẻ giống như một ma trận nhỉ.Chúng ta sẽ bắt đầu biểu diễn chúng lên ma trận nhé.
matrix = [["Hoa","Thua","Thang"],["Thang","Hoa","Thua"],["Thua","Thang","Hoa"]]
Và giờ mình cũng sẽ tạo ra một con máy random tự động trả về bao búa kéo với mình
from random import randint
print ("Quy uoc Bao :0")
print ("Quy uoc Bua :1")
print ("Quy uoc Keo :2")
lst = ["Bao","Bua","Keo"]
computer = randint(0,2)
userinput = int (input ("Moi ban nhap: \n"))
print ("Nguoi dung da nhap",lst[userinput])
print ("May nhap",lst[computer])
matrix = [["Hoa","Thua","Thang"],
["Thang","Hoa","Thua"],
["Thua","Thang","Hoa"]]
print ("Ket Qua",matrix[computer][userinput])Ok và giờ ta đã có một con máy để chơi với chúng
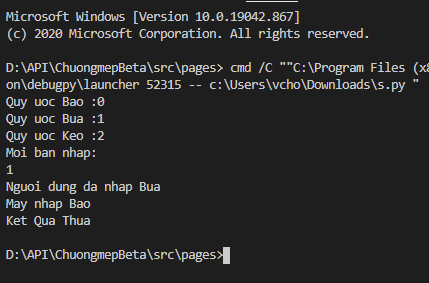
Để đỡ tốn bộ nhớ hơn, lúc này chúng lại đưa các chữ trong ma trận về biểu diễn bởi một ma trận toàn số đại diện cho giống ở trường chúng ta đã học nhé.Ở đây các con số 0,1,-1 đại diện cho 3 khổ mẫu hoà,thắng,thua.Vì thế chúng ta mới có ma trận 3x3.Cứ thế mở rộng bài toán mỗi phức tạp, chúng ta sẽ có mỗi ma trận lớn hơn và tốn thời gian hơn để giải.
from random import randint
print ("Quy uoc Bao :0")
print ("Quy uoc Bua :1")
print ("Quy uoc Keo :2")
lst = ["Bao","Bua","Keo"]
computer = randint(0,2)
userinput = int (input ("Moi ban nhap: \n"))
print ("Nguoi dung da nhap",lst[userinput])
print ("May nhap",lst[computer])
mx = [[0,-1,1],
[1,0,-1],
[-1,1,0]]
results = ["Hoa","Thang","Thua"]
print ("Ket qua",results[mx[computer][userinput]])Và cũng sẽ cho ra kết quả tương tự, điều khác ở đây chính là ma trận đã giúp chúng ta giải quyết bài toán một trò chơi vui vẻ thật nhanh phải không ?
Giờ hãy thử lại bài toán này với phương pháp của riêng bạn không dùng ma trận xem có đơn giản như thế không ?
Đi làm chúng ta làm gì ?
Có lẽ ở đây nhiều người ai cũng đã đến rạp chiếu phim để xem phim, vậy thì hôm nay mình thử cùng nhau đánh giá một bộ phim hoặc một dự đoán về bộ phim như thế nào.Đầu tiên, chúng ta sẽ có một tập dữ liệu danh sách người dùng và xếp hạng đánh giá cho các bộ phim.Nhưng mỗi người lại không đánh giá hết các bộ phim.Ví dụ có 5 bộ phim thì người dùng chỉ đánh giá 3 bộ còn lại họ không đánh giá.Nhiệm vụ của mình là sẽ dự đoán kết quả của hai bộ phim còn lại người đó đánh giá như thế nào.
Tập dữ liệu được xem như sau với thứ tự cột lần lượt : id người dùng, id bộ phim đánh giá , hạng đánh giá từ 1 đến 5
1,1,1
1,2,3
1,3,4
1,5,5
2,1,2
2,2,4
2,4,1
3,2,3
3,3,2
3,4,4
3,5,1
4,1,1
4,2,3
4,3,4
4,5,1Được rồi bây giờ chúng ta sẽ biểu diễn lại ma trận cho dễ hình dung hơn như bài toán kéo búa bao kia.Dữ liệu ở đây chính là tệp data kia nhé
f = open("data.txt")
users = []
movies = []
ratings = []
for line in f:
a =line.rstrip().split(",")
users.append(int(a[0]))
movies.append(int(a[1]))
ratings.append(int(a[2]))
f.close()Giờ thì đưa chúng vào ma trận thôi, nhớ import thư viện numpy vào để trông ma trận dễ nhìn hơn nhé.
rows = max(movies)
cols= max(users)
#Tao ma tran 0 phu hop voi so dong cot
a = [[0]*cols for i in range(rows)]
# Gan phan tu cho ma tran
for i in range(len(movies)):
a[movies[i]-1][users[i]-1] = ratings[i]
arr = np.array(a)
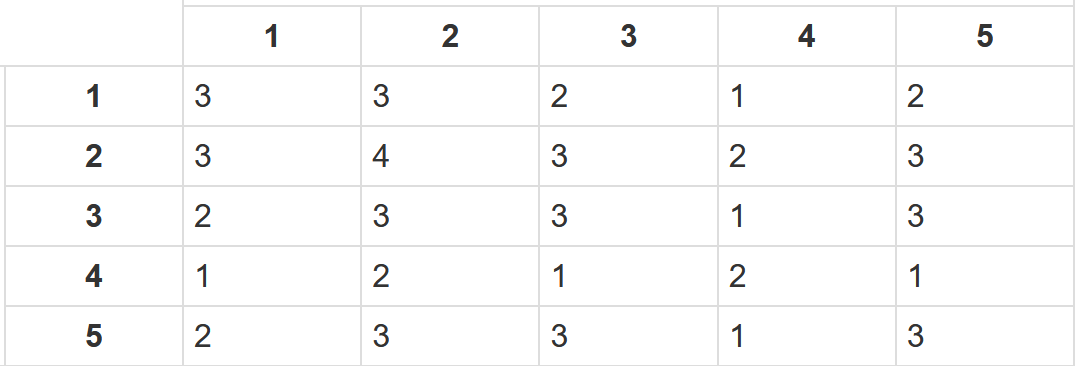
print(f"ma tran a \n{arr}")Kết quả cuối cùng ta sẽ có một ma trận trông rất dễ hiểu như thế này.Dòng đại diện cho userId và cột sẽ đại diện cho lượt đánh giá của mỗi moviesId
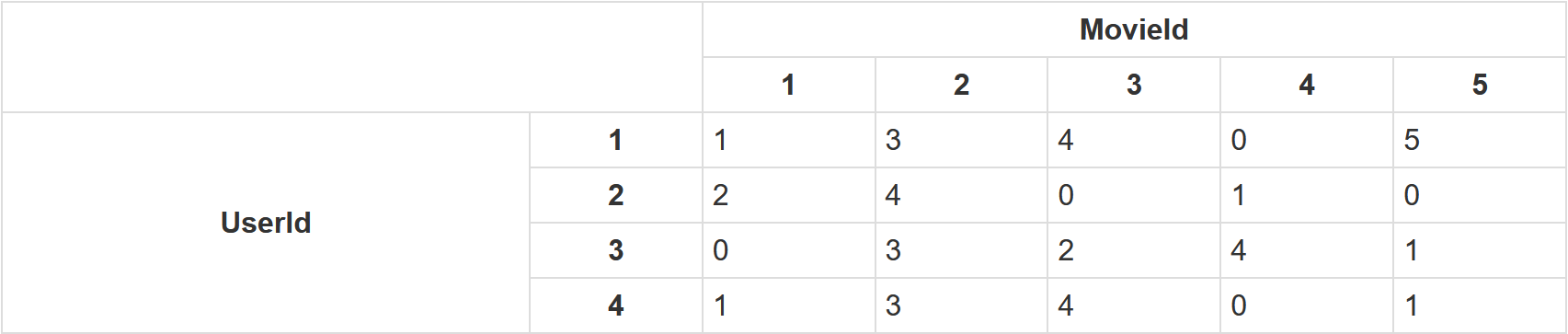
Bây giờ chúng ta sẽ tiếp tục tạo ra một ma trận hệ số từ ma trận bên trên.Từ ma trận bên trên chúng ta có thể đánh giá được việc người dùng đó không đánh giá cho bộ phim nào, các con số 0 chính là đại diện cho điều đó.Vậy nhiệm vụ tiếp theo của chúng ta cuối cùng chính là tìm lời giải cho những con số 0 ẩn mình kia.
Lúc này chúng ta sẽ nghĩ ngay đến định thức và ma trận vuông.Khái niệm định thức xuất hiện đầu tiên gắn với việc giải hệ phương trình đại số tuyến tính có số phương trình bằng số ẩn. Hệ này có một nghiệm duy nhất khi và chỉ khi định thức của ma trận tương ứng với hệ phương trình này khác 0.
Như vậy chúng ta sẽ tiếp tục tính toán phần ma trận hệ số(định thức) và sẵn tay tính luôn tổng ma trận trên dòng hoặc cột để phục vụ cho công việc chuẩn hoá vector sau này, chuẩn hoá sẽ được giải thích chi tiết ở phần bên dưới.
# Dem gia tri khac 0 hai vector
def count(u,v):
c= 0
for x,y in zip(u,v):
if x*y!=0:
c+=1
return c
#Từ ma trận (A) tạo ma trận hệ số (B)
b = [[0]*len(a) for i in range(len(a))]
for i in range(len(a)):
for j in range(i,len(a)):
b[i][j] = b[j][i] = count(a[i],a[j])
print(f"Ma tran he so : \n{np.array(b)}")
#Tìm vector (V) bằng cách tính tổng trên dòng hoặc trên cột từ ma trận (B)
def calsumrow(a):
v = [0] * len(a)
for i in range(len(a)):
for j in range(len(a[i])):
v[i]+= a[i][j]
return v
sumrow =calsumrow(b)
print(f"Tong ma tran tren dong b: \n{sumrow}")Kết quả như sau:
Ok, giờ việc chúng ta đơn giản là chỉ cần tìm ra tích của hai ma trận này.Để làm được điều này, mình cần nghịch đảo lại ma trận ban đầu đã thì mới tính được.
def transpose(a):
b = [[0]*len(a) for i in range(len(a[0]))]
for i in range(len(a)):
for j in range(len(a[i])):
b[j][i] = a[i][j]
return b
c = transpose(b)Giờ thì sẽ lấy hai ma trận nhân với nhau và chuẩn hoá cuối để đạt được mục đích cuối cùng vẫn là giải quyết những con số 0 kia, chuẩn hoá chính là đưa ma trận về lại vector đơn vị, ở đây có thể hiểu đơn giản là đưa về số hạng giá trị nằm trong vùng của số hạng đánh giá cho bộ phim.
def dot(u,v):
s = 0
for x,y in zip(u,v):
s+= x*y
return s
#1.2 tinh tich hai ma tran a*c
def mul(a,b):
d = [[0]*len(b) for i in range(len(a))]
for i in range(len(a)):
for j in range(len(b)):
d[i][j] = dot(a[i],b[j])
return d
e = np.array(mul(c,b))
print(f"tich hai ma tran \n{e}")Chuẩn hoá ma trận rất đơn giản, ta chỉ cần lấy ma trận chia cho vector.
def normalize(e,v):
for i in range(len(e)):
for j in range(len(e[i])):
e[i][j] /= v[j]
normalize(e,sumrow)
print(e)Kết quả cuối cùng mình có thể xem nhanh như sau:
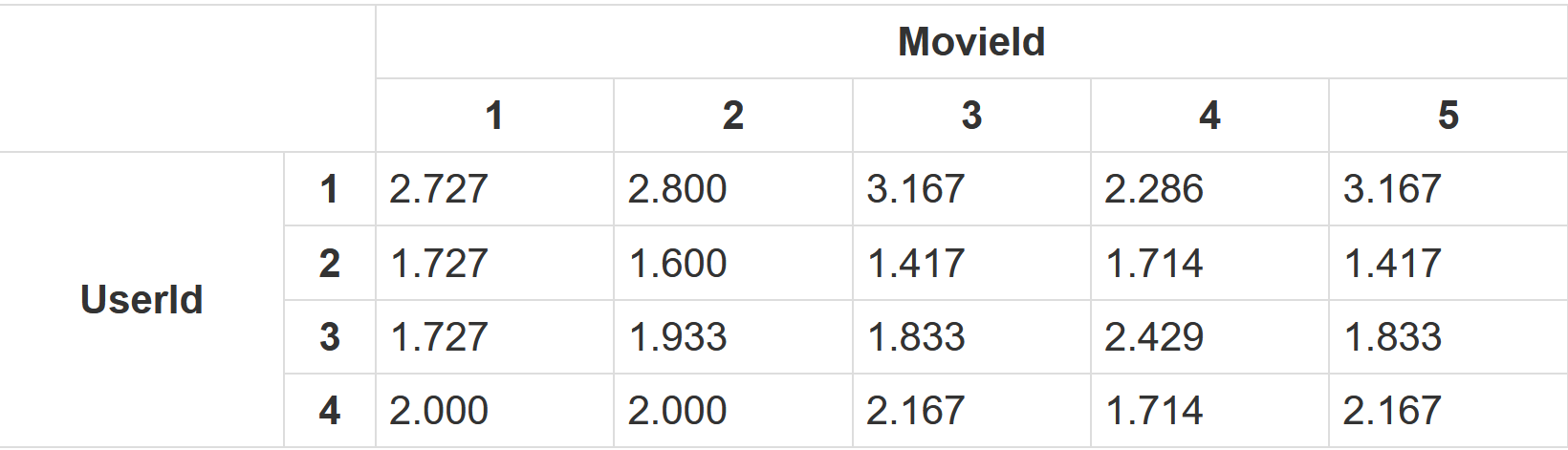
Nhìn vào kết quả, mình có thể ước lượng trước được người thứ nhất có thể đánh giá cho bộ phim thứ tư ở hạng 2.3 nếu họ có xem và cũng có thể đánh giá cơ bản cho những người còn lại.Nhưng dữ liệu ở đây khá ít nên sẽ không chính xác về mặt dữ liệu dự đoán.Với việc đó, người ta phải âm thầm lấy dữ liệu của nhiều người dùng càng nhiều càng tốt thì dữ liệu sẽ càng chính xác.Nhờ đó mà người ta có thể dựa vào đánh giá mà đưa ra quyết định nên chiếu bộ phim này một ngày mấy lần, ước lượng thu nhập của một bộ phim đạt được, gợi ý tiếp cho những phim tiếp theo nên ra mắt là gì thuộc thể loại nào,....Đến đây thì bạn đã hiểu việc thu thập dữ liệu quan trọng như thế nào rồi chứ.Việc này cũng giống như việc bạn vừa gửi tin nhắn chia tay bạn gái thì vô tình bị facebook nghe được.

Như vậy cũng tương tự với việc học trên trường học, chúng ta vùi đầu để giải quyết những con số, những lỗ hổng còn thiếu trong ma trận kia thì ở đây chúng ta cũng đang làm việc đó một cách âm thầm bằng việc tính toán các vector, đơn giản hoá chúng lại để tìm ra kết quả tính toán phù hợp.
Mở rộng
Hy vọng qua bài viết này sẽ giúp bạn phần nào đó hình dung cơ bản về một ma trận và tính hữu ích của nó.Tất nhiên không phải ai cũng được sử dụng và áp dụng vào cuộc sống hằng ngày.Tất nhiên ở trong trường học là khô khan và các bài toán đa số là để đánh đố nhau nhưng cũng đừng vì đó mà nản lòng.Hãy tìm một thứ hữu ích biết đâu bạn sẽ thích nó.
Để tìm hiểu rõ hơn về các hướng dẫn trên, bạn có thể xem qua liên kết này introduction-to-recommender-systems