Mở đầu
Bài viết này giúp bạn hình dung cách dời một điểm lên mặt phẳng trong không gian 3 chiều.Thông thường đây là một việc làm rất cần thiết và thường xuyên với các kĩ sư để áp dụng cho các bài toán cần xử lý hình học.
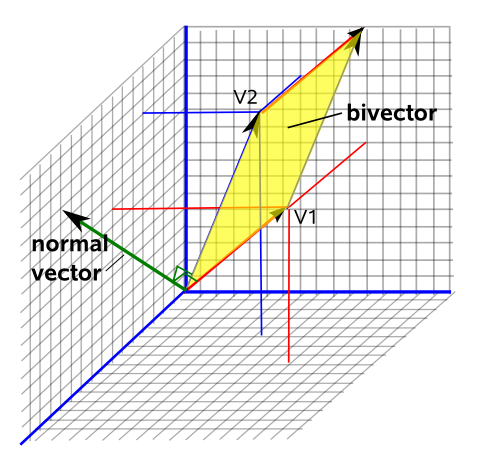
Chiếu điểm lên mặt
Hình vẽ bên dưới cho thấy không gian hệ trục toạ độ và một mặt phẳng nằm trong hệ toạ độ đó, điểm nằm ngoài kia chính là điểm mà ta sẽ dời lên trên mặt phẳng.Ví dụ bạn có một danh sách đèn cần đặt tự động.Nhưng vấn đề ở đây là không phải trần của phòng nào cũng có cao độ như nhau.Vì vậy bạn cần tìm ra chính xác cao độ trần và dời những điểm đèn đến trần. Kiến trúc liên tục dời cao độ trần làm hệ thống MEP đầu báo khói , đèn, cảm biến,.... cũng phải di chuyển theo.Nếu hai nhóm liên tục thay đổi qua lại thì việc làm tay thiếu sót là điều không thể tránh khỏi.
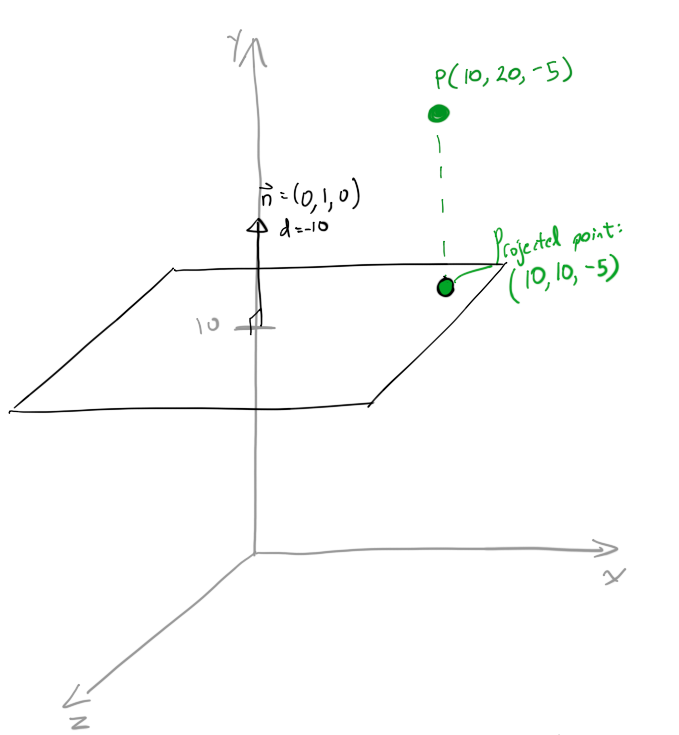
Được rồi , lúc này mình sẽ biểu diễn chúng trên Dynamo để bạn dễ hình dung hơn .Ta có hai điểm và một mặt phẳng, số 1 chính là điểm mà ta cần dời, số 2 chính là điểm sau khi được dời , còn số 3 chính là mặt phẳng mà ta muốn điểm thứ nhất chiếu lên để ra điểm thứ hai.Bạn thấy đố, điểm thứ hai chính là kết quả của việc chiếu vector vuông góc với mặt phẳng thông qua khoảng cách từ điểm đó đến mặt phẳng vuống góc với vector chiếu.
Nói một cách tổng quát:
Nếu hướng mặt phẳng được xác định bởi vectơ [a, b, c]
Khi đó phương trình của bề mặt là: a * x + b * y + c * z = 0
Để chiếu một điểm lên mặt phẳng này, chúng ta cần tính vị trí trên mặt phẳng với khoảng cách ngắn nhất đến điểm.Mà điểm ngắn nhất ta sẽ sử dụng phương pháp bình phương nhỏ nhất hay nói cách khác chính là đường vuông góc từ mặt phẳng điểm điểm cần chiếu.

Kết quả sau khi kiểm tra.Điểm nằm trên đường màu đỏ kia chính là điểm mà ta đã dời đi, điểm cần dời di chuyển ra xa bấy nhiêu thì điểm dời sẽ nằm trên mặt phẳng và di chuyển ra xa bấy nhiêu.
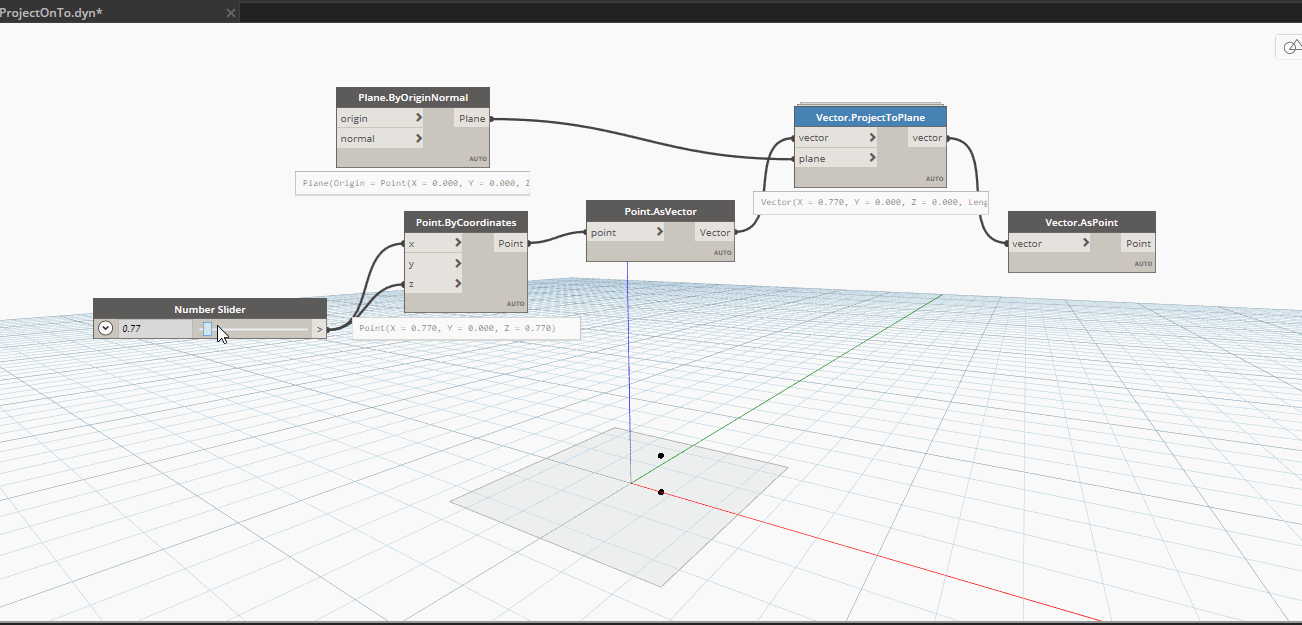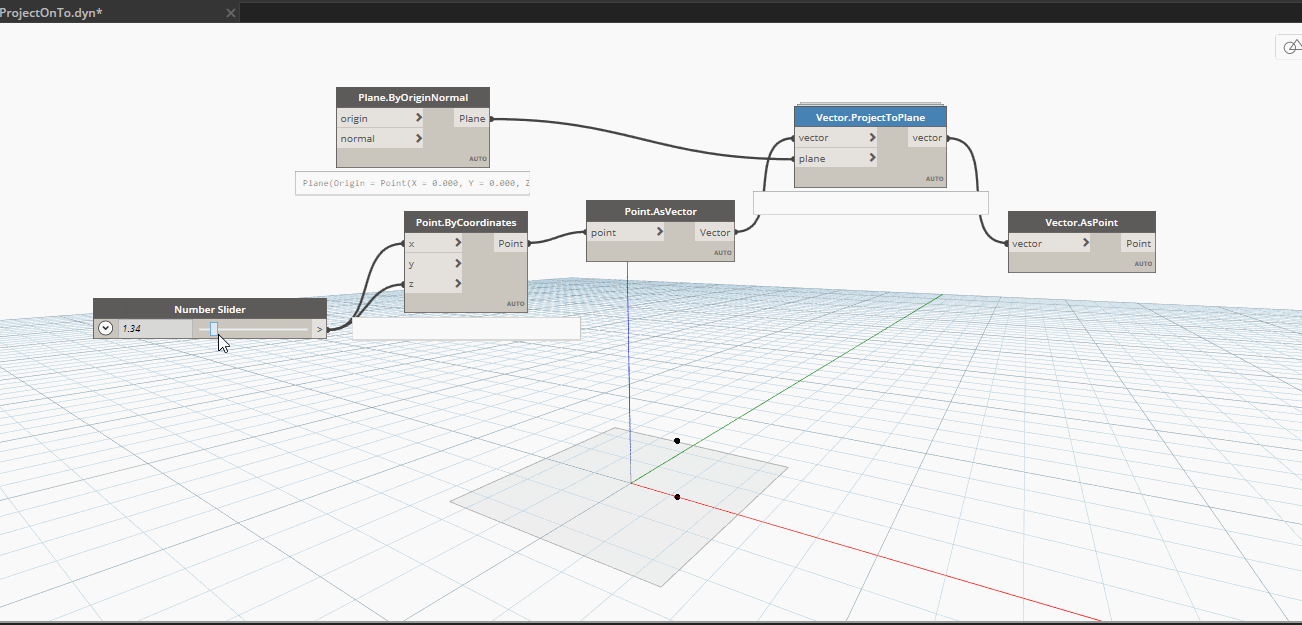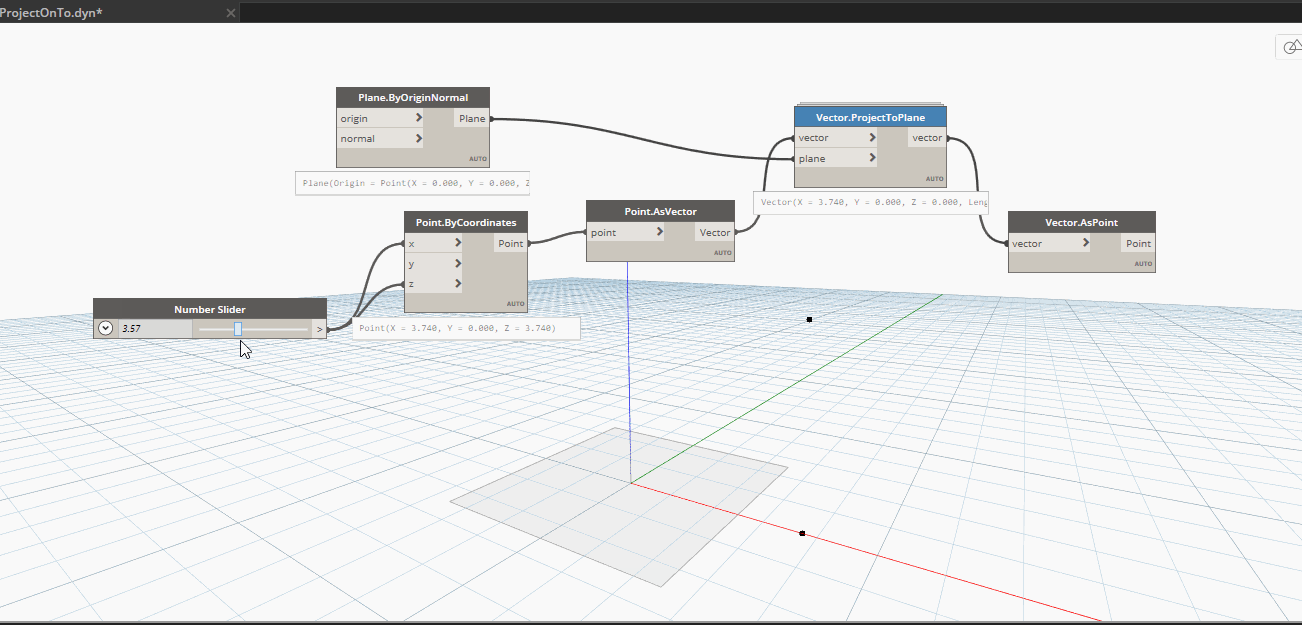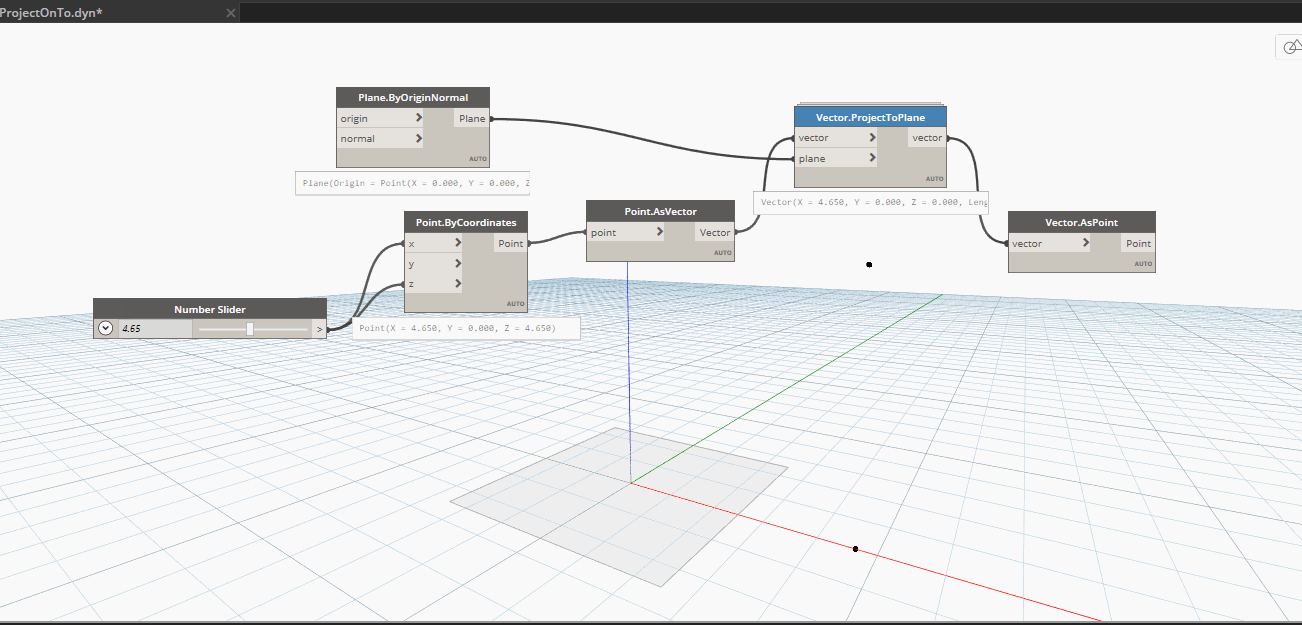
Ta có thể viết một cách ngắn gọn cho việc ta đã tìm ra điểm normar của mặt phẳng đó.
XYZ ProjectPointOntoPlane(
XYZ point,
XYZ planeNormal )
{
double a = planeNormal.X;
double b = planeNormal.Y;
double c = planeNormal.Z;
double dx = ( b * b + c * c ) * point.X - ( a * b ) * point.Y - ( a * c ) * point.Z;
double dy = -( b * a ) * point.X + ( a * a + c * c ) * point.Y - ( b * c ) * point.Z;
double dz = -( c * a ) * point.X - ( c * b ) * point.Y + ( a * a + b * b ) * point.Z;
return new XYZ( dx, dy, dz );
}Hay một cách tổng quát hơn bằng việc tính khoảng cách ngắn nhất sau đó chiếu đến mặt phẳng.
public static XYZ ProjectToPlane(this XYZ po, Plane p)
{
XYZ vecPoToPlaneOrigin = p.Origin - po;
if (!IsEqual(vecPoToPlaneOrigin.DotProduct(p.Normal), 0))
{
return po + p.Normal * vecPoToPlaneOrigin.DotProduct(p.Normal);
}
return po;
}
bool IsEqual(double a,double b,double TOLERANCE=0.00001)
{
return Math.Abs(a - b) < TOLERANCE;
}Mở rộng
Một câu hỏi của người dùng đó là tại sao nút intersect trong dynamo tại sao lại có lúc trả về point, có lúc lại trả về line ?
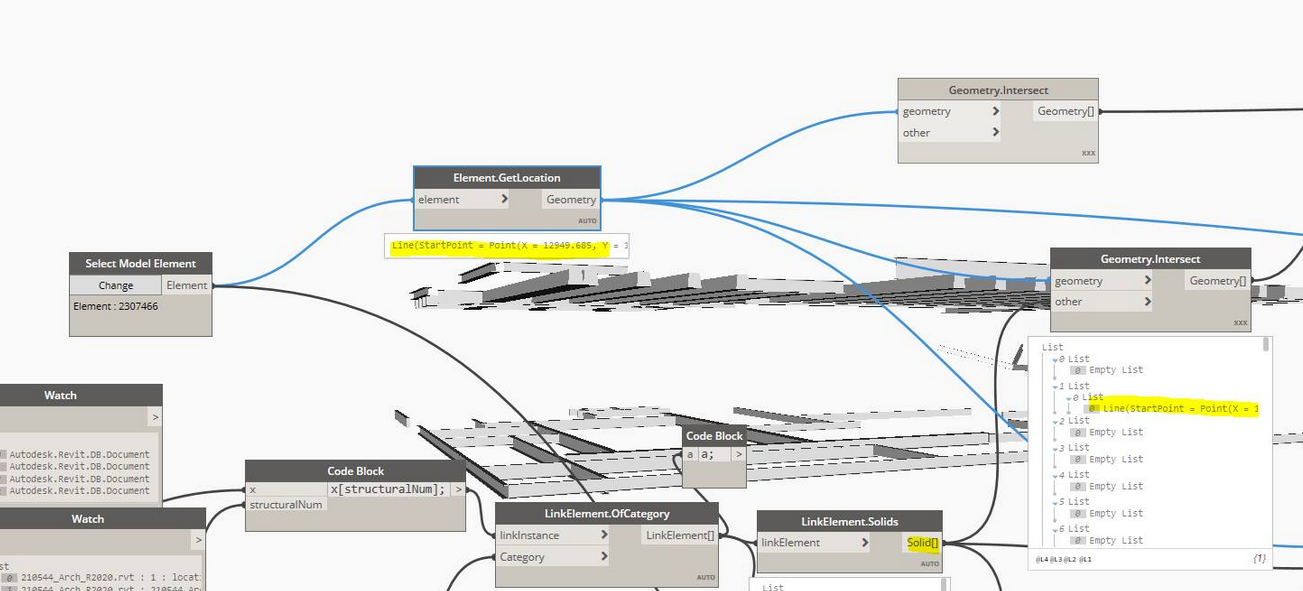
Trước tiên hiểu về intersect là gì, đó là phép tìm ra điểm giao giữa đối tượng hình học này và đối tượng hình học kia.Hãy xét một hệ quy chiếu Oxyz, hình chiếu vuông góc của một điểm vào một mặt phẳng chỉ tồn tại duy nhất một điểm chiếu, đó là phép chiếu cơ bản để tìm ra điểm giao giữa một điểm lên một mặt phẳng.Mở rộng vấn đề đó. Để tìm ra hình chiếu của một điểm với một đường thẳng ta chỉ cần chiếu điểm đó lên mặt phẳng quy chiếu của đoạn thẳng đó.Với bài toán mở rộng tìm điểm giao của một khối vuông với một đoạn thẳng ta cũng làm cách tương tự.Khối vuông lúc này sẽ bao gồm 4 mặt phẳng chiếu hướng ra tính từ 4 phía, giả sử khối vuông đang đặt nằm trên mặt đất và đoạn thằng được đặt nằm vuông góc với mặt đất và xuyên qua giữa khối vuông.Bài toán được giải bằng việc phân tách các mặt phẳng của khối vuông để giải lần lượt.Và bây giờ, bài toán đã trở thành đơn giản hơn là sẽ quy về tìm giao điểm giữa đường thẳng và mặt phẳng, ở đây chính là 4 mặt phẳng của khối vuông.Và cách giải lần lượt với từng mặt phẳng đó thông qua các bước :
- Chọn mặt phẳng chứa đường thẳng cần xem xét (Nên chọn mặt phẳng vuông góc để dễ chiếu) => Mặt phẳng A
- Tìm giao tuyến của mặt phẳng A với mặt phẳng cần xét => Đường thằng XX (tìm ra hai điểm chung của hai mặt phẳng, )
- Tìm giao điểm giữa đường thẳng XX và đường thẳng ban đầu = > Điểm cần tìm Như vậy bài toán sẽ có rất nhiều trường hợp xảy ra : Không có điểm trả về, có điểm trả về., có nhiều điểm trả về. (Empty,Point,Points=>Line,Polyline,....) Với bài toán ví dụ trên thì chắc chắc sẽ trả về Line vì đường thẳng xuyên qua hai mặt phẳng thì sẽ có hai điêm trả về, nối hai điểm trả về ta được một Line.
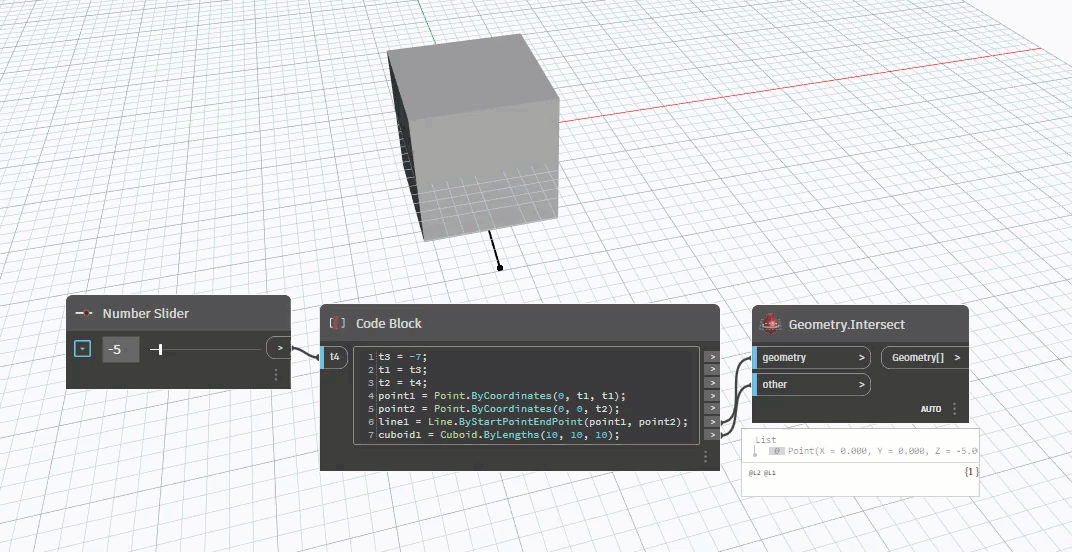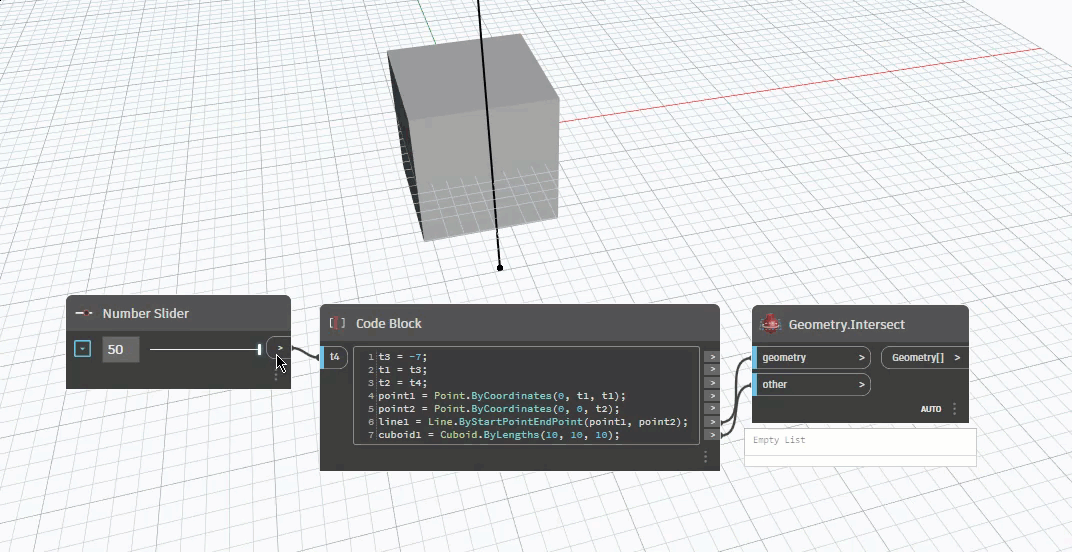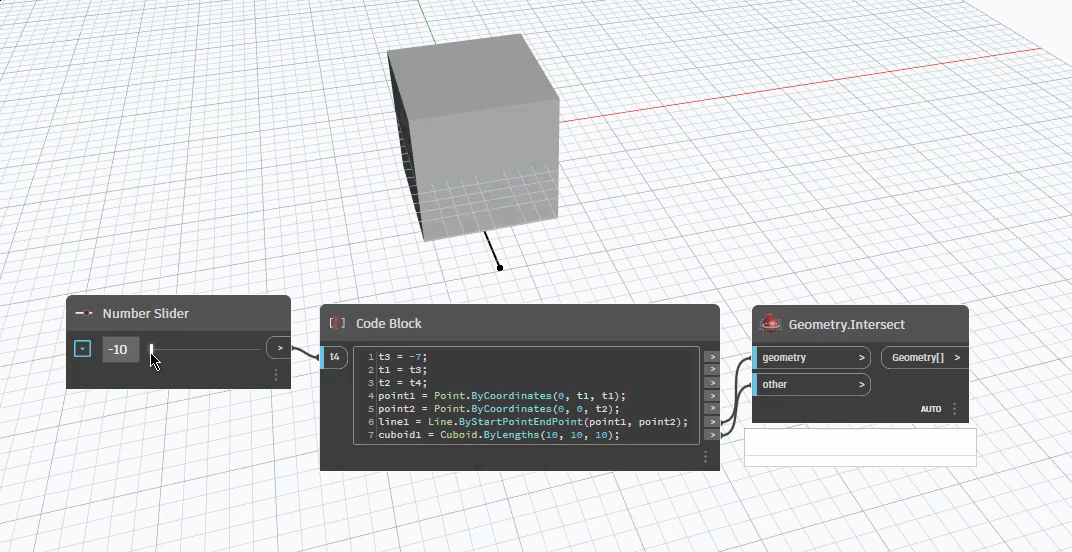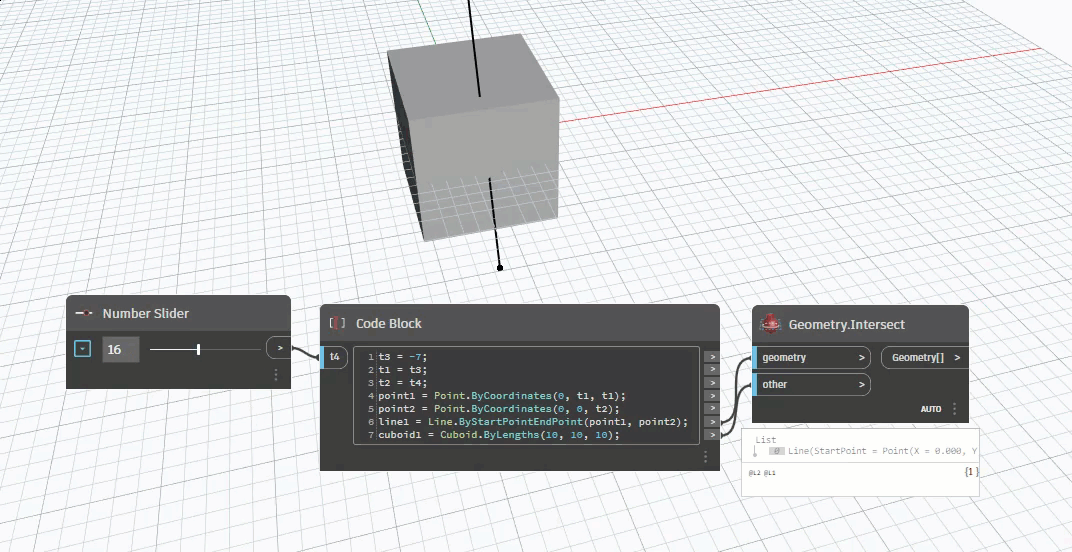
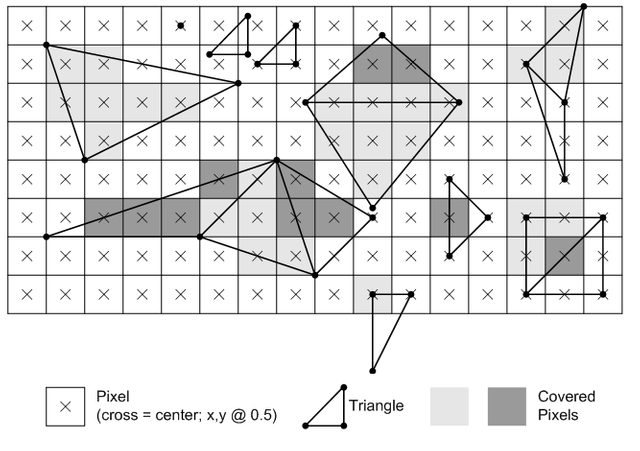
Trong đồ họa máy tính một phương pháp được sử dụng rất bổ biến đó là phương pháp dò tia, một bề mặt có thể biểu diễn dưới dạng một tâp hợp các mặt phẳng, giao điểm của một tia với mỗi mặt phẳng được sử dụng để tạo ra hình ảnh của bề mặt.Đó cũng là sự khởi đầu cơ bản để đo độ sâu của trường ảnh 3d trong thị giác máy tính dựa vào các phương pháp này, và đó cũng là lý do sự khởi đầu của các hình ảnh 3d từ việc kết nối các đoạn thẳng thành những tam giác không đồng đều đó tạo ra,..Đó cũng là sự khởi đầu của hình học 3D bây giờ.
Tham khảo
Twitter: @ColinMcCrone